What Is Draft or Draught Of A Ship?
Vessel draft or vessel draught
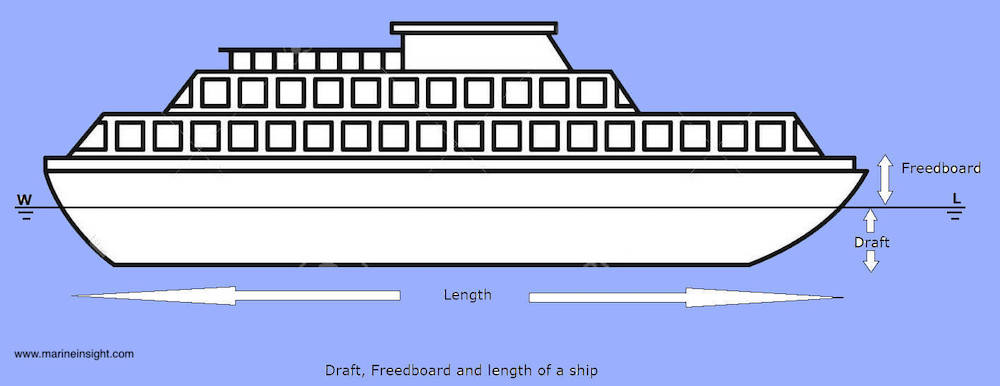
Vessel draft (draft in the American spelling, draught in the British) is one of the principal dimensions of any waterborne vessel and is defined in technical terms as the distance between the ship’s keel and the waterline of the vessel.
The keel of a ship is the lowest longitudinal support member that helps form the structure of the vessel, while the waterline of any floating body is the location on the hull of a ship where the air-water interface occurs.
The difference between the total height of the vessel and the draft is called the freeboard and is measured from the waterline to the upper deck. Simply put, the draft and freeboard combine to give the height of any vessel.
Along with the length (denoted as Lpp or length between perpendiculars) and breadth (denoted as B) of the vessel, the draft (denoted as T) is an important physical quantity that defines both the ship stability and the permissible loads that may be stored onboard without generating any adverse effects.
The draft of most ships varies longitudinally from the bow to the stern, and this results in varying drafts along the length of the vessel. Thus, the accurate manner to indicate the draft of a particular boat or ship is to mention either the location at which the draft has been measured, or whether the ship has an even keel during floating conditions.
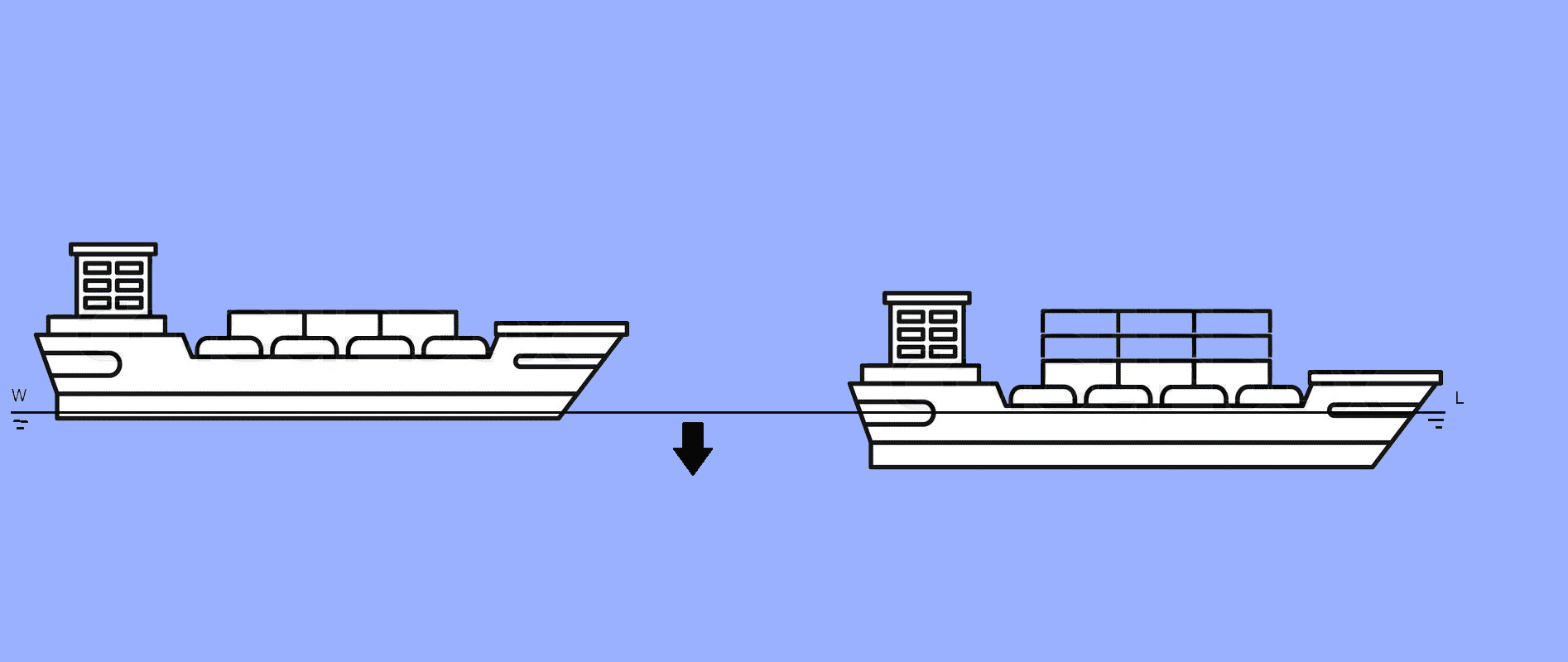
This is of particular significance when evaluating port entry regulations for any vessel since ports are always located in relatively more shallow waters than the surrounding regions.
If the draft of a vessel varies along the length but only a single draft is mentioned in the ship’s documents and stability manual, it is likely that the vessel may capsize during entry to the port due to an unstable equilibrium. Thus, it is necessary to diligently mention all the relevant drafts of the vessel in the required documents.

Importance of The Draft of a Vessel
Measuring the draft of any vessel is essential to ensuring a safe balance between the maximum load that can be stowed away on board, and the point at which the vessel is no longer stable.
Shipowners and operators attempt to maximize the onboard loads, so that they can run passenger and container ships profitably while transporting the maximum cargo possible in the least number of round trips required.
However, as the weight of the vessel increases, its draft also increases to support the increased load.
Beyond a certain point, the vessel sits extremely low in the water and is susceptible to flooding when struck by even the slightest of waves. Also, green water, which is the water collected on the deck of the ship due to waves, is prone to icing over the entire hull of the vessel in frigid environments.
The icing of the vessel can result in the engine and another machinery failing, or the loss of stability of the vessel due to the additional weight of ice.
International safety standards set the maximum and minimum drafts for these very reasons and these standards vary depending on whether it is passengers, grain, high-density material, oil or other substances being transported.
They also take into account the weather patterns along the route being sailed through and account for any changes in the physical and chemical properties of the water bodies.
Generally, cargo vessels carry full capacity loads only during certain legs of their journey and are relatively lighter during the other periods. As a result of this lack of weight, the vessel tends to rise in the water and its draft decreases. Such vessels lack integral stability due to the extreme conditions that can be brought about by a simple load addition, removal or imbalance on the deck or other regions of the ship.
Even relatively normal, natural phenomena such as waves or winds can severely compromise the stability of such vessels. Under drastic circumstances, this might even lead to the vessel collapsing.
To prevent this from occurring, inspectors and research teams from various international standard organizations such as the Indian Register of Shipping (IRS), American Bureau of Shipping (ABS), Bureau Veritas (BV), etc. inspect vessels to ensure that they conform to lightship and fully-loaded draft conditions, within a pre-set factor of safety. The data for these values comes from statistical prediction, as well as extensive calculations carried out by simulation software.
Bonjean Curves and Coefficients of Form
Another important use of the draft of a vessel is in the calculations of the Bonjean curves and certain coefficients of form. The coefficients of form such as the block coefficient (to measure how full the ship is compared to an enclosing cuboid) and vertical prismatic coefficient (to measure how full the ship is compared to a prism of height equal to the draft and cross-section equal to the waterplane area) aid in assessing the form, shape and associated hydrodynamic values of a particular vessel.
These are non-dimensional quantities that have significance in the theoretical study of the performance of the vessel while sailing.
The block coefficient, abbreviated as C(B) is given as:
C(B) = (underwater submerged volume) / (length x breadth x draft of the vessel)
The length mentioned here refers to the length between the aft and fore perpendiculars. The C(B) value can range from 1 for barges to 0.45 for high-speed crafts. Common ranges for these values depend on the source, as well as the vessel manufacturer.
Similarly, the vertical prismatic coefficient abbreviated as C(P) is given as:
C(VP) = (underwater submerged volume) / (waterplane area x draft of the vessel)
The waterplane area refers to the area which is enclosed by the waterline on the hull of the vessel. The C(VP) usually ranges from 0.99 for barges and 0.76 for certain bulk carriers to 0.39 for high-speed crafts.
In both these coefficients, the draft plays a major role in assessing the form of the vessel. Again, the common ranges vary based on the manufacturer and source.
Bonjean curves refer to a set of graphical readings that correlate several quantities with the draft of a vessel. In particular, the cross-sectional area and its moment about the baseline are mainly recorded and measured.
This is generally computed using numerical measures on simulation software and then verified by the hydrostatic testing of the vessel during its sea trials.
Whatever differences are recorded in the two measurements are then rechecked and updated. The underwater cross-sectional area, at a particular location, varies as follows:
Underwater cross-sectional area (A) = KeelTy.dz
The moment of the underwater cross-sectional area of the vessel about the baseline is given as follows:
Moment of underwater cross-sectional area (M) = KeelTz.y.dz
How to Read Vessel Draft?
Draft readings are taken by evaluating the draft measure painted on the sides of the vessel, generally near the stern of the ship. It resembles an enlarged ruler with markings and standard codes written on it. For larger vessels and ships, the draft measure might be painted at multiple locations to make it easily accessible to crew and service personnel.

For instance, most bulk carriers and tankers have six visible draft measures located at the fore port side, fore starboard side, midship port side, midship starboard side, stern port side, and stern starboard side. The fore portion of the vessel refers to the front end, the stern refers to the rear and midship refers to a point exactly midway between the length of the vessel.
Port and starboard refer to the left and right sides of the vessel, when it is viewed from the stern to the fore, or in the direction of the forward movement of the vessel.
A reason for taking the draft measures at multiple locations on the port and starboard sides of the vessel is to check whether the vessel has an inherent heel. Similarly, the draft is also measured at the fore and stern side to check whether the vessel has an inherent trim.
Such inclinations can severely compromise the vessel stability in the event of uneven and rough seas. Also, if the ship is inclined beyond a certain point, cargo and machinery might not stay stationary. Thus, it is essential to monitor the difference in the drafts at the port and starboard sides and to compute the inclination of the vessel to check if it falls within accepted standards.
The draft measure contains marker lines and readings with the depth at which the vessel is sitting for a particular load on it. These draft readings taken by using the painted measure are often referred to as apparent drafts. This is because the actual draft listed in the vessel documents may vary due to various factors such as water temperature and salinity.
Surveyors and inspectors use other instruments to measure the exact draft at which the vessel sits since the painted scale only has certain unit measures on it. To do so, the inspection team uses a boat or other small watercraft to sail from scale to scale and record the measured draft.
Draft readings are always taken into account when ship operators decide the load that a vessel will be carrying along a particular route. Occasionally, there might be small differences between the expected reading and what is observed on loading the vessel. Thus, port authorities closely monitor the draft measure during the unloading and unloading procedures, to ensure safety compliance of the vessel.
The theoretical drafts listed in the manuals for a ship are those measured at the perpendiculars during sea trials and testing periods. Vessels have two main perpendiculars that contribute to their associated hydrostatic calculations– the aft perpendicular, running through the rudder stock, and the fore perpendicular, where the hull meets the waterline.
Since these are considered to be sufficiently close to the extreme points of the ship, the drafts measured at these points are taken to be the standard for that particular vessel. Also, the draft is sometimes calculated at the halfway point along the length of the vessel, referred to as the midship draft in technical terms.
Most ships and boats tend to have markings with the maximum and minimum drafts permitted by marine standards painted along with the measure. One such mark is the Plimsoll Line, named after Samuel Plimsoll, an advocate, and pioneer for advanced safety measures to be adopted by ships sailing in treacherous waters.
It indicates the draft at which a certain vessel can float, with a certain load on it, such that it retains its stability. The Plimsoll line is an important tool in keeping the loaded cargo within the safe limits.
A basic reading of the draft measure can often be misleading since vessel hydrostatics and hydrodynamics behave differently based on varying temperature and salinity fluctuations. For instance, higher saline content in water bodies decreases the draft of the vessel due to the higher density of saltwater.
Conversely, boats sailing on freshwater bodies tend to sit deeper in the water. Thus, when setting up the draft measure, it is essential to properly assess the sailing conditions and operating environments of the vessel, and ensure that the permitted drafts satisfy safety requirements based on pre-set parameters.
Calculations Associated with the Vessel Draft
Under ideal conditions, the draft of a vessel can be simply computed by surveying the draft measure painted on the hull. In such situations, the draft remains constant along the entire length of the vessel.

However, in actual operating conditions, the vessel may be asymmetrically loaded both along the length and breadth due to various parameters based on assessments by the ship owners, operators, engineers, and captain. This uneven loading gives the vessel a lengthwise incline (known as the trim) or a sideways incline (known as the loll) and gives varying draft readings when checked using the measure at different points.
In such cases, knowing the overall incline of the vessel is essential to ensuring the stability of both the vessel and the packed cargo. Sliding and untethered cargo in the hold can cause damage to both property and people. The incline based on the draft readings can be computed as follows:
Sideways incline angle (in degrees) = arctan [| (port side draft) – (starboard side draft) |] / (required breadth)
Lengthwise incline angle (in degrees) = arctan [| (fore draft) – (stern draft) |] / (required length)
In this formula, arctangent refers to the inverse of the trigonometric tangent (often denoted as tan-1). The required breadth refers to the breadth of the vessel in an upright condition, at the level, hold or deck at which the required incline is to be calculated.
The breadth that is usually taken into account is the breadth at the upper deck, which is one of the standard principal dimensions of any vessel.
Similarly, the required length refers to the length of the vessel in an upright condition, at the level, hold or deck at which the required incline is to be calculated. The length that is usually taken into account is the length between perpendiculars, since this where the fore and aft drafts are measured. This is also another standard principal dimension of a vessel.
Similarly, other important quantities are the mean draft and the midship draft, which are used to compute the overall trim and heel of the vessel. Trim refers to the longitudinal dynamic motion of the vessel, while heel refers to the transverse motion. The mean draft can be calculated as follows:
Mean draft = [(draft at fore) + (draft at stern)] / 2
The midship draft is computed by measuring the draft at the midship marker painted on the side of the hull. If the drafts measured at the port and starboards differ, the average of both their values is taken for quick calculations. The midship draft and mean draft do not have to be necessarily equal.
Based on the type of carrier, they can vary over wide ranges. For instance, high-speed crafts and small motor-powered boats have different values of their mean and midship drafts. However, larger vessels such as tankers, carriers and container ships all tend to have more or less similar values for the two types of drafts.
The accurate way of measuring the draft and recording it in the log and manual of the ship is by mentioning all the locations at which the draft is measured, their readings, as well as certain values such as the inclinations to port, starboard, fore, and stern.
Also, the ship’s stability manual must list out the varying drafts at accepted and general levels of cargo, and how they can vary with the density of water. Lastly, the actual draft readings of the vessel must fall well within the permitted range set by international and national standards organizations.
What are Draft Surveys?
Draft surveys refer to the studies or calculations that utilize the measurement of the draft of a vessel for the main purpose of measuring its weight based on any condition of loading. This is achieved by having these surveys make extensive use of the draft readings and measurements of the vessel, either from the stability manual or from the physical readings of the measures painted on the side of the hull.
The reason draft surveys are required is that computing the weight of large vessels such as container ships and carriers is practically impossible using known methods. In addition to this, companies often want to quickly measure the weight of the cargo they are loading on, without having to individually measure the weight of each package or good. This is where draft surveys come in, by saving both time and money.
By using the existing knowledge of the shape of the vessel from the manual and documents in conjunction with the Archimedes Principle of floating bodies, the weight of the load on any vessel can be computed. According to the Archimedes Principle, the weight of a body floating in water is supported by the volume of water that it has displaced. Essentially, it can be written as follows:
Weight of vessel in kg = (Volume of water displaced by the vessel in m3) x (Density of water in which the vessel currently is in kg.m-3)
Also, the volume of water that has been displaced by the vessel while on the water is numerically equal to the underwater submerged volume of the vessel. The underwater submerged volume can be computed using the Bonjean curves. Thus, the formula for the weight of the vessel can be rewritten as:
Weight of vessel in kg = (Underwater volume of the vessel in m3) x (Density of water in which the vessel currently is in kg.m-3)
The density of water changes from place to place, depending on several parameters. As a result, it is important to measure the density carefully at the given location while computing the weight.
Now, with the knowledge of the weight on the vessel at any given point of time, it is possible to compute the weight of cargo that has been loaded by the ship as follows:
Weight of cargo in tonnes = (Weight of fully loaded vessel in tonnes) – (Weight of empty vessel in tonnes)
Tonnes are the general units of weight for huge bulk carriers and tankers. Since the density varies with location, it is important to measure the empty and loaded conditions of the vessel at the same place, and not from different locations.
In Conclusion
Thus, we can see that the draft of a vessel plays a crucial role, not only in assessing the stability and form of the vessel but also in draft surveys and other useful computations.
The main points to be kept in mind while reviewing the draft of any vessel are that the draft can vary along the length, the draft at a given condition changes depending on the type of water, and the draft has implications on the incline and weight calculations.
By combining the Bonjean curves of a given vessel and its stability manual, a thorough understanding of how the draft affects the performance of the vessel is possible. It is also important to ensure that the values of draft fall well within the pre-set safety ranges to ensure the overall stability of the vessel.
Do you have info to share with us ? Suggest a correction

About Author
Ajay Menon is a graduate of the Indian Institute of Technology, Kharagpur, with an integrated major in Ocean Engineering and Naval Architecture. Besides writing, he balances chess and works out tunes on his keyboard during his free time.
Latest Naval Arch Articles You Would Like:
Subscribe To Our Newsletters
By subscribing, you agree to our Privacy Policy and may receive occasional deal communications; you can unsubscribe anytime.













Excellent article. The Second Link bridge over the Johor Strait is 25 m above high water. Making the Strait a shipping lane is planned. What size ship could use such a navigation channel? I would be most grateful for you input. Thank you
(or an email to me.)