Understanding Draft Surveys – Importance, Calculations & Errors
The draft of a vessel (spelt as draft in the American system or draught in the British system) is a measure of the distance between the surface of the water which meets the hull of the vessel, commonly termed as the waterline, and the keel or baseline of the vessel, which is the lowest member running in a longitudinal direction that provides support and structure to the shape of the hull.
The draft (denoted by T), the length between the fore and aft perpendicular, referred to as the length between both perpendiculars (Lpp or Lbp), and the vessel’s breadth at the upper deck (B) are commonly taken as the principal standard dimensions of a vessel. These provide important results and conclusions about the hydrostatic forces, as well as aiding in draft surveys.
What are Draft Surveys?
Simply put, draft surveys are any calculations or studies carried out, which record the draft of a vessel for the primary purpose of measuring its weight in any condition of loading.
To do so, these surveys make extensive use of the draft readings of the vessel, either from the stability manual or from the physical readings of the measures painted on the side of the hull.
Draft surveys enable ship operators, owners and engineers to conveniently calculate various important quantities without investing significant amounts of time on trivial computations. This saves both time and money, which are equally important for cargo and passenger-carrying vessels.
The revenue made by these companies relies on maximising the cargo shipped in the least amount of possible time, and at the least cost.
In such cases, the weight being transported plays a major role in carrying out optimisation studies. Also, for warships and other ancillary military vessels, these draft surveys are significant in ascertaining the speed, turning ability, propulsion and possible resistance faced by the ship while sailing. This is done by taking into account the weight of any additional machinery or weapons that are present either on or below the deck.
For such vessels, the localised loads of machinery vary rapidly, and care must be taken to ensure that due to the high-frequency oscillations and weight of the weaponry, the deck and flooring are suitably reinforced. The weight of the individual machinery can be measured like that of the cargo.
Another important reason for carrying out draft surveys is to ensure a vessel is stable before being allowed to dock at any port. Unstable vessels are prone to collisions while in port or may even capsize while sailing, costing millions of dollars in damage and loss of revenue to both the parent company and the country of docking.
This is why port authorities diligently conduct inspections to ensure that no such untoward incidents take place.
How are Draft Surveys Carried Out, and by Whom?
Draft surveys are generally carried out by inspection teams and safety officials belonging to either the parent company of the vessel or the port at which the vessel is currently docked.
These officials are tasked with inspecting the manifesto, goods, passenger and crew records, documents of the vessel, and the safety standards. Another important task of these officials is to measure and verify the draft values of a vessel.
The inspectors responsible for ensuring the safety and stability standards use small watercraft or boats to get around the ship, inspecting for any damage or wear and tear on the external hull, propellers, and rudder.
Also, they check and note down the draft readings as measured at the multiple scales painted on the sides of the vessel. These painted measures are generally located at six major points for medium to large size vessels- fore port side, midship port side, stern port side, fore starboard side, midship starboard side, and stern starboard side.
The forward section of the vessel is referred to as the fore or bow, the rear portion as the aft or stern and midship to the section which divides the vessels length into two halves.
Similarly, starboard and port are nautical terms referring to the right and left halves of the vessel, when viewed in the forward moving direction of the vessel, or from stern to fore.
In general, while carrying out draft surveys, the fore and stern drafts are taken into consideration. Since a permanent tilt of the deck of a vessel can be dangerous, corrections are made in the loading so that the port and starboard drafts match.
The points at the fore and stern where the drafts are measured refer to the fore and aft perpendiculars. These are 2 imaginary lines that pass through the vessel and serve as reference points for various calculations.
The aft perpendicular passes through the rudder stock of the vessel. The fore perpendicular passes through the foremost point on the hull where it intersects the waterline.
Mathematically, computing these drafts result in the most accurate values due to their relative position with the midship and centre of floatation.
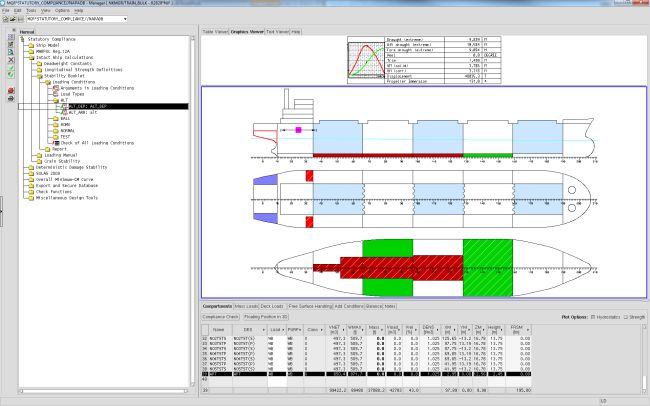
Once the preliminary readings are taken, these are then cross-checked with the values noted in the stability booklet of the vessel. Along with this, the weight of the vessel is then calculated using the Archimedes principle.
Since this requires the correct density of the water in the port, a sample survey of the water is routinely conducted so that any fluctuations can be monitored.
On completion of the survey, the vessel is given a certificate of clearance from the port officials and is allowed to either enter the port or continue on her journey.
Draft Survey Calculations: Calculating the Weight of a Vessel
Calculating the weight of a vessel is necessary on several counts, as outlined in the previous section. However, unlike normal modes of transport, measuring the weight of the load on board a ship is much more complex. Certain vessels transport easily measurable cargo, such as container ships.
Container ships have the individual weight of each container available in the manifesto of the ship and the sum of the weights of the individual containers results in the final weight of the cargo being transported.
Similarly, oil tankers can compute the weight of oil loaded based on the volume and density of oil, and their associated calculations. Such weights are calculated as follows:
However, bulk carriers that carry grain, ore or other loosely placed items are more difficult to assess. The draft of a vessel helps to measure the total weight that the vessel has taken on by utilizing the Archimedes Principle of hydrostatics. Briefly put, the weight of a body is directly proportional to the volume of water that is displaced when it is submerged or floating.
The volume of water that is displaced is equal to the underwater volume of the vessel. The underwater volume of the vessel can be computed from the Bonjean curves that are computed during the manufacturing and design process.
Bonjean curves are mathematical plots unique to every vessel that graphically depicts how the cross-sectional area, its moment of inertia and the total submerged volume vary based on the draft.
The Bonjean curves are mentioned in the trim and stability manuals of every vessel, and are computed as follows:
In the above formulae, x, y, and z represent the three coordinate axes that define a 3D volume. The length of a ship is generally taken about the x-axis, the breadth is taken about the y-axis, and the draft is taken about the z-axis.
The origin is found on the centre plane, at the intersection of the keel and aft perpendicular.
In the unloaded condition, we can measure the weight of the vessel without its cargo by using the draft to assess the volume of the portion of the vessel that has been submerged.
On measuring the draft again, but in the fully loaded condition, we can find the total weight of the vessel when loaded with cargo. By computing the difference between the two weights, one can easily find the weight of cargo that has been taken on board a vessel.
We have to keep in mind any deductible weights that can vary throughout measuring the weight. These include fuel levels, ballast tank levels and other non-essential fluids that can be measured using a sounding technique of their storage tanks.
The aim is to weigh the vessel in a lightship condition its cargo so that the most accurate weights are recorded.
Using the Archimedes principle, we can compute the total weight of any floating body as follows:
Weight of the body in tonnes = [(Submerged volume of the body in m3) x (Density of water in kg.m-3)] / 1000
Then, by computing the weights at both loading conditions, we can get the weight of the cargo as follows:
Weight of cargo in tonnes = (Weight of fully loaded ship in tonnes) – (Weight of empty ship in tonnes)
By taking into account any deductible weights, we can rewrite the corrected equation as:
Corrected weight of cargo in tonnes = (Weight of fully loaded ship in tonnes) – (Weight of empty ship in tonnes) – (Weight of deductible loads)
Similarly, for military warships, to calculate the weight of individual machinery, we compute the weight of the vessel when the weaponry is not loaded, and then again when it has been loaded. By comparing the weights at both conditions, we can get the weight of the weaponry as follows:
Weight of weaponry in tonnes = (Weight of ship with a weapon in tonnes) – (Weight of empty ship in tonnes) – (Weight of deductible loads)
The weight of ships and boats are usually measured in tonnes, because of the large magnitude of quantities used in their measurement.
Another point to keep in mind is that the density of water changes depending on various factors such as temperature and salinity. This has to be taken into account when computing the weight of the vessel.
If the vessel has been weighed at one location in the unloaded state, measuring its fully loaded weight in another location might not yield accurate values due to the difference in salinity.
For small crafts and high-speed boats, this does not make a major impact in the calculations, and a constant value is usually taken depending on the operating conditions.
On the other hand, for tankers and bulk carriers, this value could translate to a few hundred kilograms or more, because of the sheer size of these kinds of vessels.
Possible Sources of Error
When computing the weight of any item, errors creep in either due to operator, instrument or other unavoidable inaccuracies. For conventional road transport such as trucks and cars, this does not pose a major problem.
However, when it comes to the case of vessels, small calculation mistakes translate to considerably large errors because of the sheer size of ships and boats.
Even a few millimetres off from the accurate value can result in a difference of several hundred kilograms due to the large size of such vessels.
The most common source of error that might result in wrong values for either draft or weight measurement arises from instruments that have been inaccurately calibrated and set up.
To calculate the draft from the measures painted on the sides of the ship, scales are used to accurately determine where the vessel sits on the water.
Since these measures only contain base units and certain values, it is up to the inspection teams to further compute the exact draft. However, when instruments are inaccurate, the wrong values of the draft may be recorded in the manuals of the vessel.
The other source of error in the calculation of draft surveys is operator error. Due to the nature of the location of the draft measures on the sides of the hull of a vessel, approaching them while the boat is either moored at a port or stationed away from the quay can be extremely tricky.
Large propellers on the aft of the vessel make it dangerous for individuals to take the measures unless they are properly trained in handling their instruments. As a result, minute errors can emerge while calculating the draft surveys.
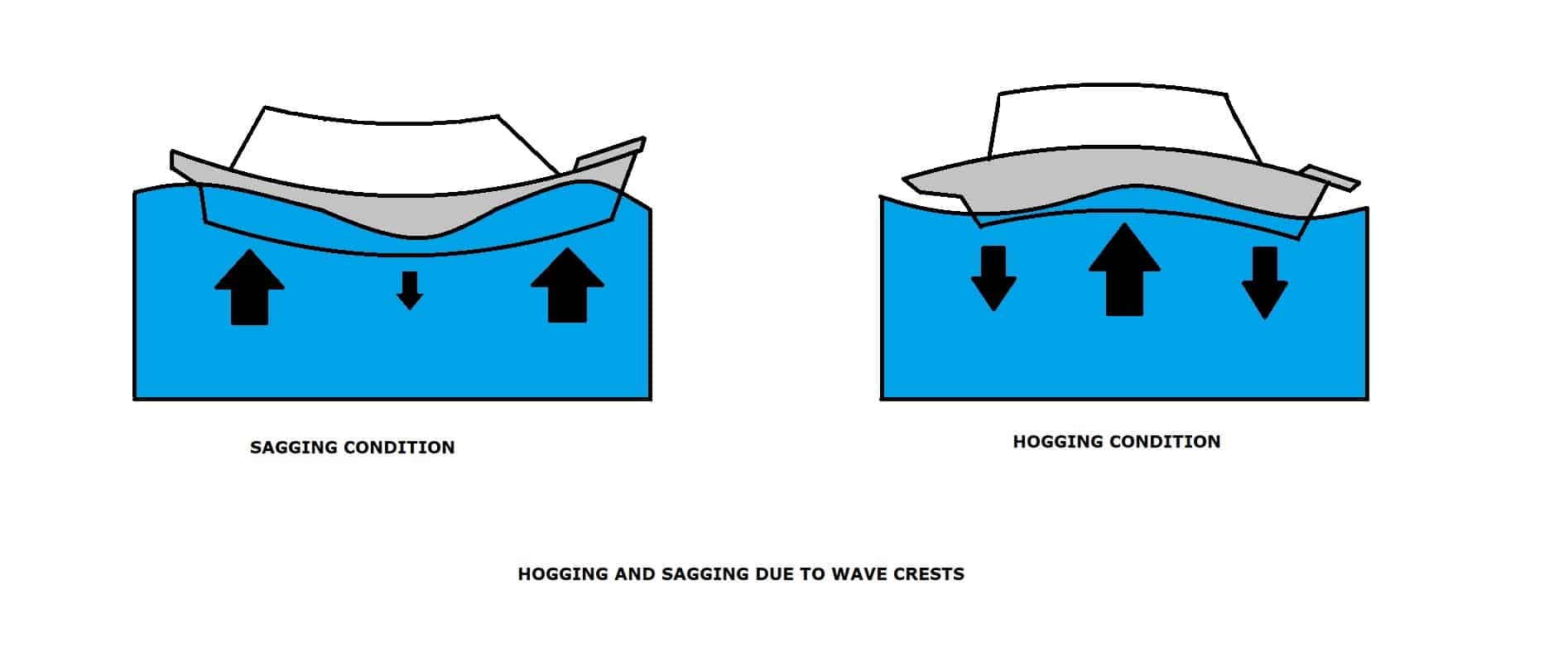
Hogging or sagging of the vessel is another source of error that occurs due to unavoidable circumstances. This error results in different sections of the vessel having a considerable difference in the drafts, due to structural fatigue in the hull.
In general, the weight of a ship is not evenly distributed along the keel. This is because essential machinery such as the engines and shafts are located at the stern of the ship so that they can efficiently transfer power to the propellers of the vessel.
However, this results in an imbalance of weights between the stern and fore due to the additional load at the aft. Moreover, during the loading and unloading processes carried out, the weight distribution can be skewed. Since the force of buoyancy is dependent on the weight distribution along the length of a vessel, these sections tend to create a bend in the hull of the vessel, known as hogging or sagging.
Hogging occurs when the midship section of the vessel has a lower draft than the fore and aft sections and is termed as being concave to the water surface.
Sagging occurs when the midship section of the vessel has a higher draft than the fore and aft sections and is termed as being convex to the water surface.
Another reason for hogging and sagging is the presence of waves. Hogging occurs when the midship is located at the crest of a wave, and sagging occurs when the midship is on a trough.
To prevent this from happening at ports, breakwaters are constructed along with the entry so that they dampen incoming waves and ensure a still water condition.
Since any such large-scale computations are prone to error, necessary measures have to be put in place so that it can be minimized. Also, in the event of any drastic weather conditions, vessel stability must not be affected.
To do this, the production company that carries out sea trials and tests on the completed lightship provides the vessel operators with a safety range of load weights.
Within this range, the integral stability of the vessel is not upset by the additional load weight. However, at values outside this range, the stability may be compromised.
Captains and ship operators are required by international standards and laws to keep the load on the ship below the pre-set value.
Conclusion
This manner of computing the weight of any vessel in any state of loading by utilizing draft surveys saves the operator both time and money. Such a procedure measures individual loaded and stored goods redundant and unnecessary. Instead, by simply using the Bonjean curves in conjunction with the draft surveys, the weight of cargo in any condition can be computed.
Moreover, in a world where technology plays a major role in fast and efficient interfaces, sensors play a major role in measuring the draft of a vessel and then relaying the information back to the main servers housing the electronics of the ship.
From these readings, the weight is instantly calculated and conveyed to the operators in real-time. This helps monitor the vessel weight and draft status during entry into ports or during storms when the ship runs the risk of capsizing due to uneven load distribution.
Disclaimer: The authors’ views expressed in this article do not necessarily reflect the views of Marine Insight. Data and charts, if used, in the article have been sourced from available information and have not been authenticated by any statutory authority. The author and Marine Insight do not claim it to be accurate nor accept any responsibility for the same. The views constitute only the opinions and do not constitute any guidelines or recommendation on any course of action to be followed by the reader.
The article or images cannot be reproduced, copied, shared or used in any form without the permission of the author and Marine Insight.
Do you have info to share with us ? Suggest a correction
Latest Naval Arch Articles You Would Like:
Subscribe To Our Newsletters
By subscribing, you agree to our Privacy Policy and may receive occasional deal communications; you can unsubscribe anytime.
Web Stories

About Author
Ajay Menon is a graduate of the Indian Institute of Technology, Kharagpur, with an integrated major in Ocean Engineering and Naval Architecture. Besides writing, he balances chess and works out tunes on his keyboard during his free time.




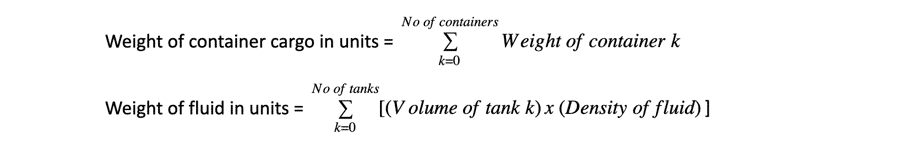










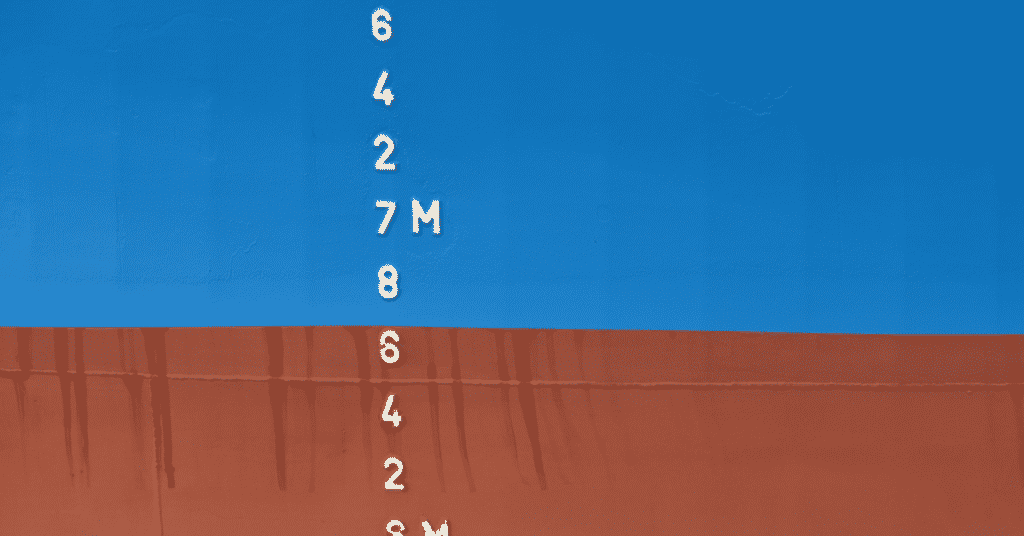





Sometimes, tricky operators, rolls slightly the ship, previously to finish the cargo operation.
When the draft surveyor finish, balance the tanks again