What is Reserve Buoyancy in Ships?

At the start of this article, let us go back to the basic concept of flotation and buoyancy.

How and why does anybody float in water?

A finite-sized body floats in water by displacing or supplanting a certain amount or volume of water or the medium it is in.

Returning to the classic example of a floating cuboidal box (with dimensions as L, B and D, respectively), the body floats in water by displacing a certain volume of water medium (having extents as l, b, and t) underneath.

From the first principle, the weight of this displaced volume of water is the same as the body’s physical weight. Hence, the displaced volume of water, by Newton’s third law, imposes a force on the floating body, which is mathematically equal to the body’s weight and acting in a direction above that is opposite to the weight action.

Reserve Buoyancy

This creates a physical equilibrium or a balance of forces that keeps the body afloat without sinking.

The overall scenario is named Archimedes’ principle of floatation. The amount of water displaced by the body that weighs the same as the body itself and balances the body by applying an equal and opposite force, as this weight is termed displacement. And the equal and opposite reaction force upwards that keeps the body afloat is known as buoyancy.

The equivalence of this buoyancy is a function of the following:

Geometry
Form
The density of the object
The density of the medium

By this, we mean that the nature of the floating object should be of size, density, and form such that the volume of water displaced and hence, the equivalent amount of buoyancy or the upward balancing force offered basis on the weight of the displaced volume should be sufficient to create the situation of static equilibrium to keep the body afloat.

For example, when we place a body like the above-mentioned box or a flat metal plate or a metal tray on water, we see it easily float. However, when we place a solid metal ball or a brick on the water of the same weight as the above objects, it immediately sinks.

Why? This is because the density or the mass per unit volume for a metal ball or a brick is much higher than the density of the water body, whereas, for the tray or hollow block of metal, the body’s density is lesser than that of the water.

Moreover, the form and the geometry of a tray or a box are such that the volume of water that can be displaced is greater; hence, the weight of this displaced volume of water that yields an equivalent amount of balancing upward force is sufficient to make the bodies float.

Reserve Buoyancy

By virtue of the body’s form, the upward buoyancy is uniformly distributed over the outer surface. So, the weight or the material properties of the body is irrelevant.

The density and geometry are. Now, from the point of view of density, other than the density of the object, the density of the medium is also crucial. As we know, seawater has more density than freshwater. Hence, the same object, when floating in freshwater, needs to displace more water than seawater.

Why?

The answer, once again, lies in the corresponding densities. Seawater has a higher density than freshwater. To balance the floating body, the water medium must supply an opposite force equivalent to the body’s weight.

What is weight? The product of density and volume. Since the density of seawater is greater than freshwater, the corresponding volume that the body must displace to achieve the same equivalence in weight must be lesser than that in freshwater as from the below equality.

For the same reason, we never sink in the Dead Sea, even if we do not know how to swim! The density of the water body is so high due to the abnormal levels of salinity that even a smaller amount of displaced volume is enough to support our weight by buoyancy forces.

Ships, as we know, are defined by this same set of principles and theories. The hull displaces a definite amount of water, known as volume displacement. This can also be measured in terms of mass, as the mass of water equals the vessel’s weight.

The buoyancy forces arising from the weight of the vessel and the equivalent water displaced is uniformly distributed over the outer hull such that the vessel stays afloat.

Depending on the aforementioned factors, only a definite portion of the hull displaces water to create buoyancy enough to support the vessel’s weight. In other words, a certain part of the hull remains submerged under the waterline, and some remain above water level.

Now, we are all familiar with the concept of the depth of a vessel.

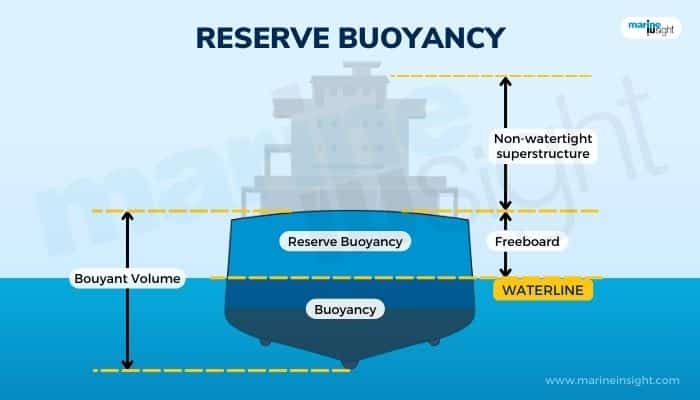
Depth is nothing but the vertical distance from the baseline or the lowermost point of the vessel to the maximum level of the main deck, weather deck, or strength deck.

The distance from the baseline to the waterline is known as the draft.

The balance length of the depth from the waterline to the maximum height of the main deck is known as the freeboard. This freeboard is an indicator of the remaining amount of clearance or the margin before there is deck flooding and subsequent water ingress.

Reserve buoyancy is the volume equivalent of freeboard.

What does this mean?

This means that the remaining space volume of the enclosed main hull above the waterline indicates reserve buoyancy.

It can be expressed as the ratio or comparison of the hull’s volume above water to the net watertight volume of the main hull.

Reserve Buoyancy: (Volume of the hull above the draft line or waterline)/ (Total enclosed hull volume)

Once again, the hull displaces some amount of water to attain the required displacement and hence, the required buoyancy forces. For ships, the volume displacement is defined as the volume of the submerged watertight enclosed hull.

Now try to understand this carefully. By nature, any finite body in a medium displaces an equal amount of volume or space as itself.

So, we are displacing an exact amount of volume of our surroundings as our own. Similarly, for a vessel floating at a definite draft, the amount of water displaced equals the enclosed volume of the hull involved in the displacement action.

As a simplistic example, if you consider a box-shaped barge of length, 20 metres, breadth, 8 metres, depth 3 metres, and floating at a draft value of 2 metres, what is the displacement?

As expected, the volume displacement would be the product of length, breadth, and draft, as 20X8X2=320 cubic metres.

In other words, the vessel has displaced the same amount of underwater volume as the enclosed hull volume of its submerged part.

If we multiply this volume in cubic metres by the density of the water, that will yield mass displacement, which is nothing but the physical weight of the entire vessel.

In almost every vessel, the hull form is typical of its design and is characteristic of some curvature. Hence, like the simple barge example above, the displacement cannot be found out from the first principles. However, with the help of numerous methods, we can deduce this quantity of displacement in both terms of weight and volume.

Going back to the problem of the simple barge, can you now tell what should be the reserve buoyancy?

The answer is simple. The difference between the total watertight hull volume and the volume involved in the displacement that is part of the submerged hull volume till the draft, divided by the total watertight hull volume.

So, in this case, it is:

[20 X 8 X 3=480 m3 (total hull volume) – 20X8X2=320 m3 (hull volume till draft line/volume for displacement) = 160 cubic metres]/ [480 cubic metres (total volume)].

This gives 33.33% of a reserve buoyancy by percentage.

This can also be easily calculated using the same length, breadth, and the difference between the depth and draft, i.e., [20 X 8 X (3-2) = 160 cubic metres]/480 cubic meters.

So, for actual ships, as per the given figure in transverse view, the part of the intact and watertight hull above the waterline represents the reserve buoyancy.

So, what is the significance? As the name suggests, reserve buoyancy is the balance amount of buoyancy that the vessel can offer.

As we know, depending on the weight of the vessel and the loading conditions and the water medium, the vessel experiences sinkage till a particular draft. The balance of the depth above the draft line is the freeboard.

However, if the loading increases or the vessel experiences some damage or flooding and faces a ‘loss in buoyancy,’ what happens? The vessel sinks further, and the draft increases. In these cases, essentially, the hull sinks for an increased volume of displacement to cater for the adequate buoyancy required to keep the vessel afloat.

Hence, reserve buoyancy essentially serves as a margin for providing extra volume displacement by sinkage and accommodating more buoyancy to keep the vessel afloat.

In the barge example, the vessel still has an allowable margin of 160 cubic metres or 33.33% of its volume to stay afloat. Or in other words, due to additional loading or some loss in the hull, the vessel can sink a maximum of another metre and cater to the buoyancy forces to attain equilibrium.

Henceforth, we can also say that this barge can have a maximum displacement of 480 cubic metres by volume. In simpler words, 66.66% of the volume already contributes to the displacement, and a maximum of 33.33% of usable volume can still be utilised. Beyond this, the vessel shall defy the condition for static equilibrium for flotation and sink after being unable to cater to the required buoyancy.

Reserve buoyancy is a very crucial yardstick for the seaworthiness of a vessel.

The extent of the reserve buoyancy determines the safety limit or margin before the vessel can sink.

The greater the reserve buoyancy, the safer the vessel is regarding sinkage, and vice-versa. For fully-loaded operations in commercial ships, the displacement is maximum, and in this condition, the reserve buoyancy is dramatically reduced.

During external conditions like high tide levels, the effect is again more pronounced. So, for a ship designer, from the early stages, the vessel should have the optimised maximum cargo or tonnage capacity only after maximising the reserve buoyancy limits to the highest feasible extent.

Bigger cargo vessels like tankers, bulkers, and even containerships have low reserve buoyancy limits under full-load conditions compared to passenger or defence vessels and hence need to be operated more carefully.

The problem of reserve buoyancy further increases in freshwater conditions due to the lower density of freshwater (and a higher draft of the vessels).

Reserve buoyancy is not always practical or possible to measure accurately or assess but can be easily deduced from freeboard.

You might also like to read-

Do you have info to share with us ? Suggest a correction

About Author

Subhodeep is a Naval Architecture and Ocean Engineering graduate. Interested in the intricacies of marine structures and goal-based design aspects, he is dedicated to sharing and propagation of common technical knowledge within this sector, which, at this very moment, requires a turnabout to flourish back to its old glory.