Understanding Block Coefficient Of A Ship

We all know that the hull form of a vessel varies widely from design to design. A small tugboat has a different hull form from a container vessel or a tanker. The hull form of a vessel is intrinsic to the type, size, build, and of course, the utility or purpose of a vessel.

Some vessels may be short and wide like tugs; some may be long and slender like high-speed navy frigates or destroyers. Some may be large and bluff, like tanker or bulk carriers. This hull form of the vessel depends on several physical parameters like length, breadth, or draft. Moreover, the hull form’s overall curvature makes the description complete.

Now, from a qualitative point of view, we may describe or comment on the hull form of a vessel. But do we have any form of quantitative measure? The answer is yes. The basic parameters or attributes of a ship, like length, breadth, depth or draft, are not enough to characterise the hull-from of a vessel due to its typical curvature that is the end-point of a designer.

So, quantitative measures comparing the different features of hull geometries under consideration with some standard reference of the convention is a good technical way of studying the hull form of any vessel.

Thus, in the field of naval architecture, the form coefficients are of very high importance. These form coefficients quantitatively describe a hull with a reference physical or overall geometric benchmark from a design and a mathematical point of view. These form coefficients are applicable in every area, like structure, stability, hydrostatics, resistance, propulsion, seakeeping, manoeuvring, etc.

Some commonly used form coefficients are Block Coefficient, Waterplane Coefficient, Prismatic coefficient, and Midship Section Coefficient. Read on to find out about the most basic of them, which is the Block Coefficient.

What is a Block Coefficient?

Now, we know that a vessel floating in water displaces a certain volume of water which imparts an opposite reaction known as buoyancy which keeps the body afloat. This upwardly acting buoyancy equals the weight of the underwater volume displaced by the hull from the first principles.

This weight of the displaced water is also mathematically equivalent to the vessel’s structure and is defined as the displacement of the vessel. The displacement is a characteristic of the hull form and it depends on the physical features of the hull, as this only translates to the volume of water being displaced at given conditions.

Once again, as we have said, the hull form is very typical for a particular vessel. So, a measure or an index of its understanding can be well deduced if we physically compare it with a simple, cuboidal block at the same levels of immersion. What does that mean? We all know, for a vessel, along with a definite length and breadth, the draft defines the height or the level till which the hull is underwater.

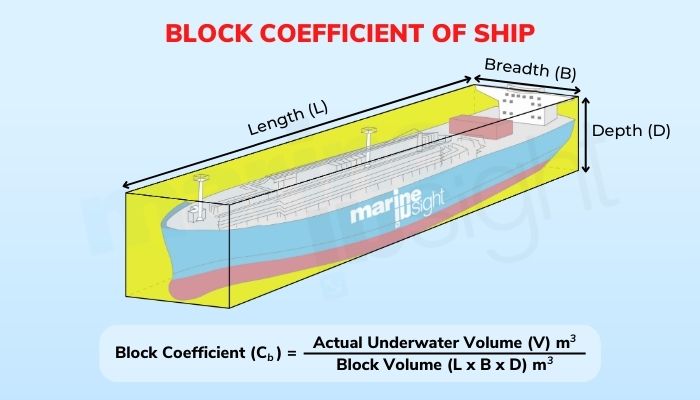
What is a Block Coefficient

Also, recall that the design breadth of the vessel is the maximum breadth, usually at midships for conventional designs. So, the underwater volume of displacement at the same draft of an equivalent block or cuboid would be the product of the vessel’s length, its width or breadth, and the present draft at which it is floating. The length used in the denominator term is the measured Length between Perpendiculars or LBP for all practical purposes.

Hence, the block coefficient is the mathematical ratio between the actual volume displacement of the given vessel and the volume displacement of an equivalent cuboid having the same dimensions at that particular draft.

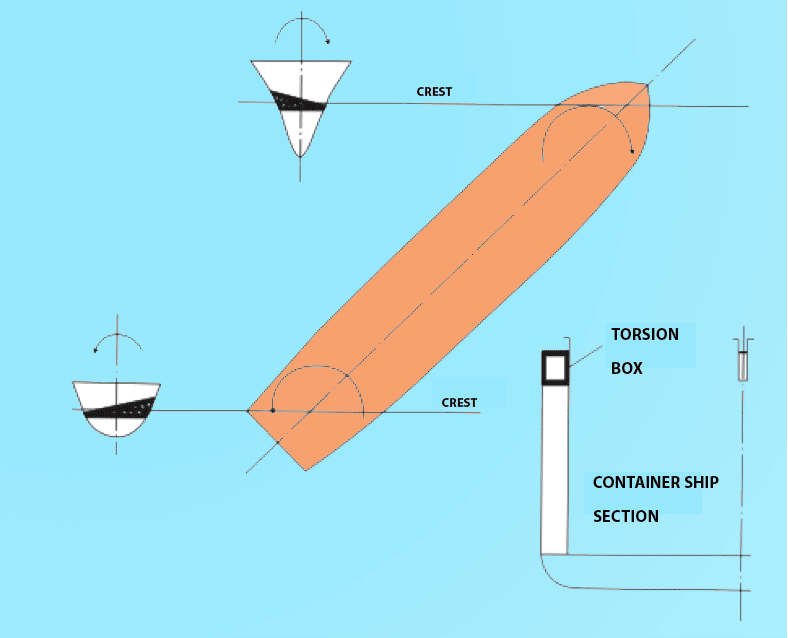
Mathematically, it is the volume displacement measured for that vessel divided by the volume of the rectangular cuboid of equal length, draft, and breadth. As per the figure below, in a visual sense, if a cuboidal or rectangular box is imagined to be exactly fitted around the submerged portion of the hull, it is equal to the ratio of the space occupied by the hull volume to the ratio of the circumscribing box.

The value of the block coefficient or CB always falls in the range from 0 to 1. This value essentially defines the fullness or fineness of the hull form. For higher values of CB, the vessel’s hull form is said to be fuller, and for lower values, it is said to be finer. For example, military fighter vessels like high-speed corvettes or frigates have block coefficients as low as 0.5-0.6.

On the other hand, fuller-form cargo vessels like bulkers and tankers have block coefficients in the range of 0.8 to 0.9. In near-ideal cases, a dumb barge or a pontoon has a block coefficient of nearly one as they closely resemble the rectangular cuboid with or without some minor deviations.

So, what brings about this block coefficient ratio for vessels?

The answer lies in the nature of the hull form once again and all the curvatures in geometry like deck outlines, bottom curvatures, turns of bilges or the bottom region, shapes of the side shell-like flares and tumblehomes, and hull shape characteristics in the longitudinal direction like the forward or aft rakes, rises, or other various forms typical to the hull form. In conventional vessels, the maximum amount of deviation is observed towards the forward and aft regions of the hull for all practical purposes.

block coefficient ratio for vessels

However, in some typical designs like escort tugs, some offshore vessels and research vessels, or several ice class ships, where there is a higher level of hull curvature towards the front of the midship region, that is, the vessel’s longitudinal centre of gravity being skewed forward, the block coefficients may be fairly high, and the block coefficient value is mostly affected by the part of the hull aft.

For passenger vessels and containerships, where there is a requirement for higher speed and hence have finer entrances shoulders, have a relatively lower value of block coefficient, not more than 0.7-0.75.

Uses of Block Coefficient

First and foremost, the block coefficient is used to have an understanding of the nature of the hull form designers, viz., the hull is finer or fuller form. Consequently, from a resistance point of view, the resistance of the hull is directly proportional to the fullness and vice-versa. This, in turn, is related to the speed of the vessel. Hence, to achieve a higher value of speed, the block coefficient must often be altered by the designers.

Similarly, to reduce power consumption or achieve higher propulsive efficiency, the block coefficient is an important parameter that is considered by designers. On the other hand, the block coefficient also essentially translates to the usable volume or tonnage of the vessel. Hence, while considering all the factors of resistance and powering, this should also be optimised accordingly.

However, in high-speed vessels with low block coefficients, the displacement-to-rule length ratio should be kept low to avoid high degrees of wave resistance.

You may also like to read-

Do you have info to share with us ? Suggest a correction

About Author

Subhodeep is a Naval Architecture and Ocean Engineering graduate. Interested in the intricacies of marine structures and goal-based design aspects, he is dedicated to sharing and propagation of common technical knowledge within this sector, which, at this very moment, requires a turnabout to flourish back to its old glory.