Ship Stability – Understanding Curves of Static Stability
Having discussed the basics of intact stability of surface ships, we are now at a stage to analyze the same. The easiest and handiest tool for analysing a surface ship’s stability, is by graphs or curves. In fact, a ship designer or an officer on-board should be able to know the stability characteristics of a ship just by looking at the curves.
Since the stability of a ship can be directly commented on by the nature and value of its metacentric height (GM), a direct method to track the stability of a ship for a range of heel angles would be, to generate a curve that relates this parameter to the angle of heel. Since metacentric height is directly related to the righting lever (GZ) and angle of heel, the curve of static stability is a plot between the righting lever and angle of heel.
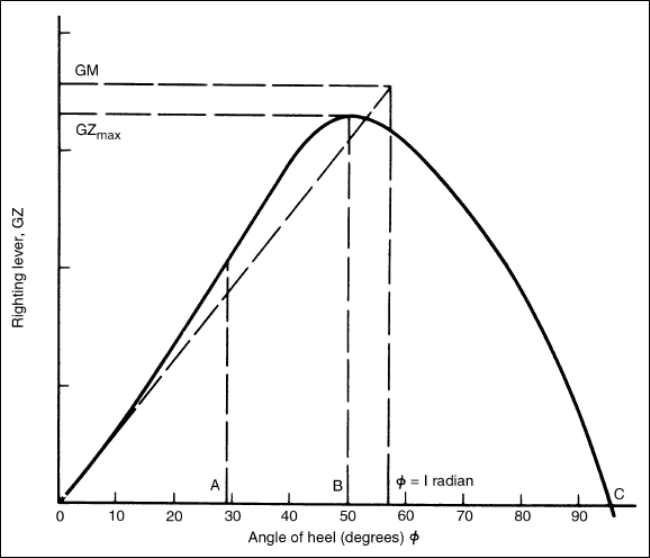
The above graph is plotted assuming that the ship is in static condition. Some of the important information that can be derived from any GZ curve of a ship are discussed below:
- If the curve intersects the origin, it means that there is no righting lever when the ship is upright. In other words, the ship has inherent positive initial stability.
- The maximum righting lever (GZMAX), represented by point ‘B’ in the graph is proportional to the largest static heeling moment that is required to bring the ship back to its upright position. The value of maximum GZ and the angle at which it occurs, are important values. In other words, the maximum righting lever when multiplied with the displacement of the ship, gives us the value of the maximum heeling moment that the ship can sustain without capsizing. Why? Because, beyond this angle, the righting lever (in other words, the stability) of the ship decreases drastically.
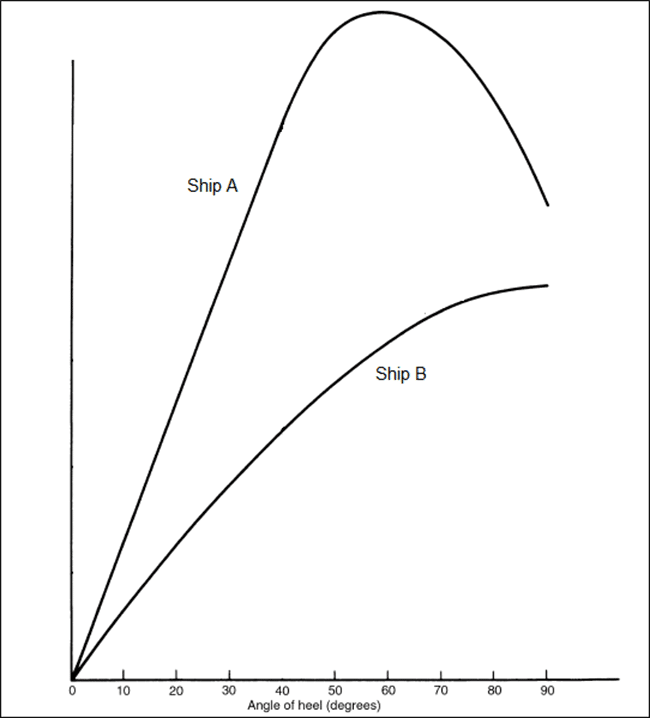
- The point where the GZ curve meets the horizontal axis (shown as ‘C’ in the figure), is called the point of vanishing stability, since righting lever becomes zero at this point. So, any heel beyond this angle would result in a condition of negative stability. The distance between the origin and point of vanishing stability is called the range of stability of a ship. In the above case, the range of stability is from 0 degrees to some angle above 90 degrees. For example, it is evident, in Figure 2 (below), that though Ship A has higher value of maximum GZ than Ship B, Ship A has a lower range of stability. Thus, Ship B will be able to heel to a larger angle before attaining negative stability.
- As the angle of heel increases, there comes a point when the deck of the ship immerses. This angle is called the angle of deck immersion, and the corresponding point on the curve is called point of inflection. How do you recognise this point just by looking at a GZ curve? To know this, let’s first understand the phenomenon of deck immersion from a stability point of view. When the deck of a ship immerses, the rate of shift of center of buoyancy (and also the righting lever) with further heeling changes. This results a change in concavity of the curve. This can clearly be noted at point ‘A’ in the above curve.
Point of inflection does not play an important role in operational purposes, but it helps designers to make preliminary predictions regarding what changes in stability would be brought about if the design of a hull-form is altered.
- The total area under the static stability curve gives the amount of energy that the ship can absorb from external heeling forces (winds, waves, weight shifts, etc.) till it capsizes. Thus, it should not be assumed that a ship is stable enough only if the value of the maximum GZ is high. A GZ curve with a very high maximum value might not have the sufficient area, and as a result, the ship will capsize easily because it wouldn’t be able to absorb enough energy before capsizing.
- If a tangent is drawn to the GZ curve at the origin, and an ordinate is drawn at 57.3 degrees (1 Radian), then the point of intersection of the tangent and the ordinate would give the value of the initial metacentric height of the ship, as shown in the above figure. This can be proved mathematically, but instead of going into that, we will understand how this important property of the curve is applied for practical purposes.
The above theory implies, that steeper initial slope of the GZ curve would mean that the ship has more initial stability. However, larger initial stability does not imply larger values maximum righting lever and range of stability. This can be depicted by studying the nature of the GZ curves of two ships (A and B), as shown below.
Angle of Loll:
It may so occur that the initial metacentric height of the ship becomes negative. As a result of this, the ship is not stable in its upright condition, leading to a heeling moment, as shown in part (a) of Figure 3 below.
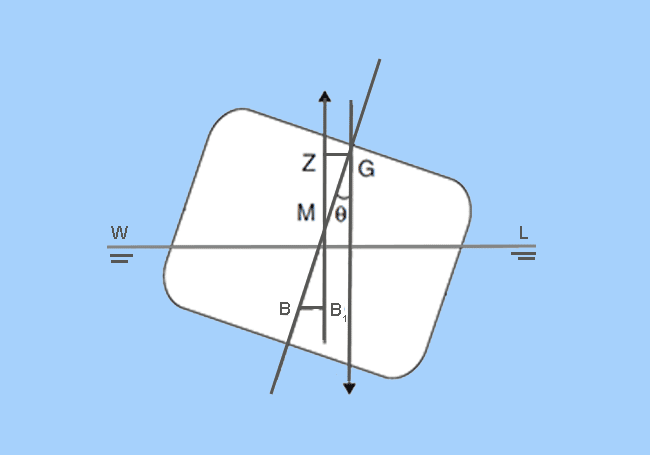
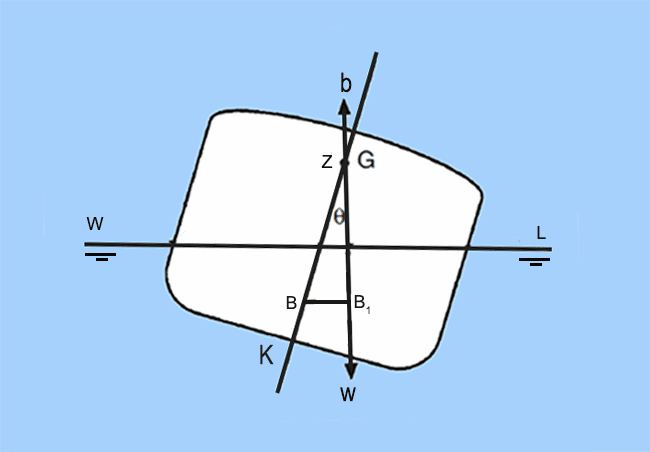
As a result of the negative righting lever (GZ), the ship heels further upto an angle where the righting moment and righting lever, both, become zero. This angle at which this condition is achieved is called Angle of Loll, as shown in part (b) of Figure 3. The important thing to visualize here is that a condition of loll can be treated as a shift of the GZ curve from the origin (shown in Figure 4 below).
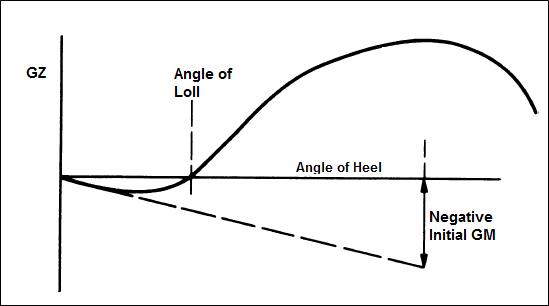
Now, when the ship heels to an angle more than that of the loll angle (part C of Figure 3), a positive righting moment is generated, which brings the ship back to its equilibrium position. However, as long as a condition of loll prevails, the equilibrium condition will not be achieved when the ship is upright. This results in a permanent angle of heel in the ship, which is an unwanted situation.
There are many reasons behind a condition of loll. One of the most commonly occurring ones is the free surface effect. We will study that, and the other causes of loll in later articles, and also see how they can be corrected. The important thing to note now, is the shape of the curve. For a designer, it is very vital to observe the initial slope of the stability curve of a ship in all loading conditions, because often, the negative slope might not be as exaggerated as shown in the above figure.
Study of Curvature of GZ Curves:
GZ curves are generated taking into consideration multiple conditions for one ship, during the design process. Though the values traced by the curve may be different in each case of loading, but the shape or curvature of the curve will hardly change, because it depends on the geometry of the hull. So, the hull designer must always study the initial curvature of the GZ curve once it has been generated for a single load case. Why and how?
Let’s consider two ships (A and B) having the same metacentric height, but different hull forms, such that the curvature of the GZ curve near the origin for Ship A is concave upward and the curvature for Ship B is concave downward as shown in figures 5 and 6 respectively. For each ship the GZ curves are plotted for:
- Loadcase 1: Normal Departure Condition (low CG) / Sufficient GM.
- Loadcase 2: When CG is higher, or GM is reduced.
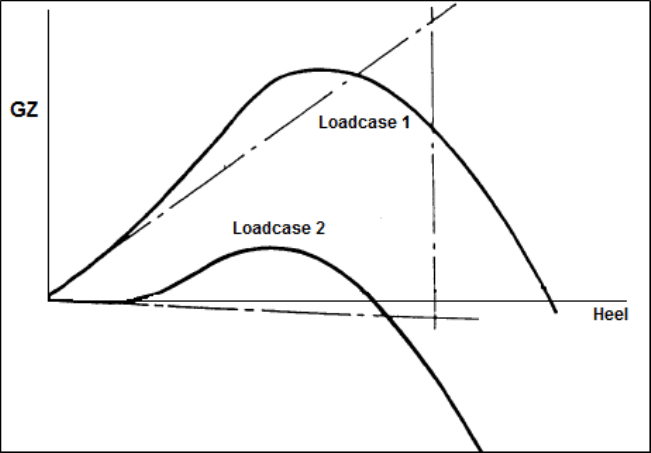
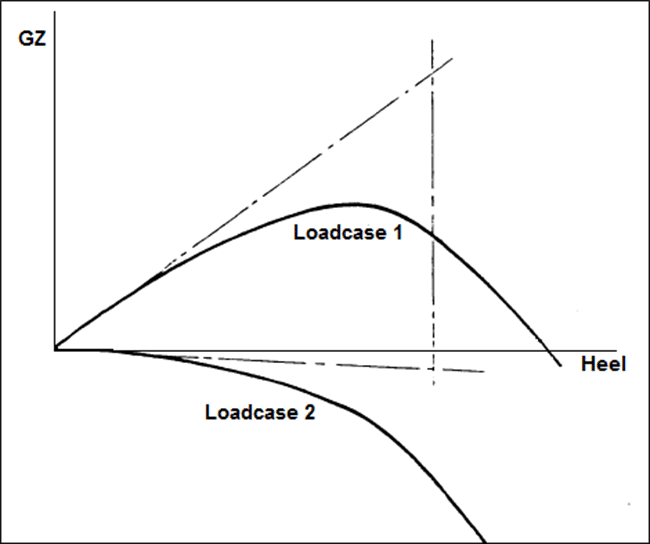
In case of both the ships, if an identical rise in centre of gravity is considered (which brings us to Loadcase 2 from Loadcase 1), the GZ reduces due to reduction in metacentric height. But both the ships would respond very differently due to the initial curvature of their GZ curves. In case of Ship A, even when the initial metacentric height becomes slightly negative (notice the initial slope for Loadcase 2), the ship will heel upto a certain angle, but as the ship keeps heeling, due to the convex upward curvature of the GZ curve the righting lever becomes positive again. This causes the ship to return to a condition of positive stability.
But in case the initial metacentric height of Ship B is even slightly negative, even a slight heeling moment will capsize the ship. Why? Because as the angle of heel increases (follow Loadcase 2 for Ship B), the righting lever remains negative due to the convex downward curvature of the GZ curve. When such a GZ curve is obtained during design phase, the designer must iterate the design of the hull. Probable methods of correcting the shape is by increasing the beam, or adding a flare, etc.
Cross Curves of Stability / KN Curves:
The vertical position of centre of gravity (G) of the ship is not always fixed. It changes with every voyage, depending on the loading conditions and the amount of ballast. The CG of the ship also changes when the ship is in transit. This varying nature of CG makes it difficult for the designer to assume the loading conditions at which GZ curves should be obtained, because different values of KG (vertical centre of gravity) would result in different metacentric heights (GM), and since righting lever (GZ) is directly related to GM, the stability curves for each of the loading condition would be different. So how do we circumvent this problem?
In order to make things easier, a few known facts were considered before developing the concept of cross curves of stability:
- KG will vary according to the loading condition.
- The KG of the ship is always known to the designer, and also the ship’s captain, for every loading condition.
- The angle of heel at any condition is also known to the designer and the ship’s captain.
The cross curves of stability were developed, so that, for any loading condition (where KG is already known), values of righting lever (GZ) can be obtained for all angles of heel.
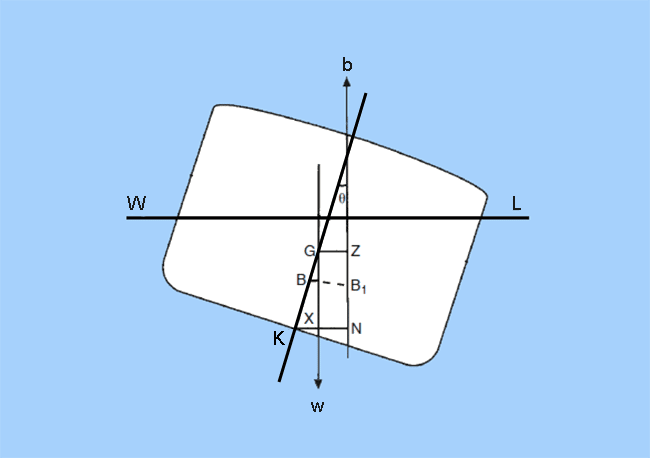
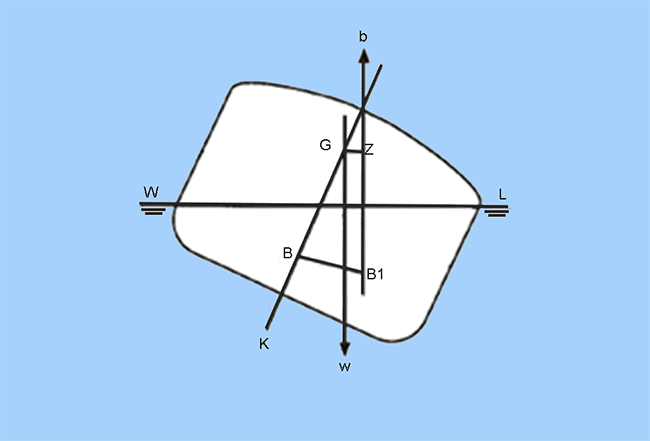
In order to understand how, study the above figure. The point ‘K’ represents the keel of the ship. If at any angle of heel (Ɵ), a line parallel to that of GZ is drawn from ‘K’, then the point of intersection of this line with the vertical line of action of buoyancy, is represented as ‘N’.
From the above figure, the following expression can be derived for righting lever: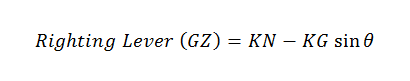
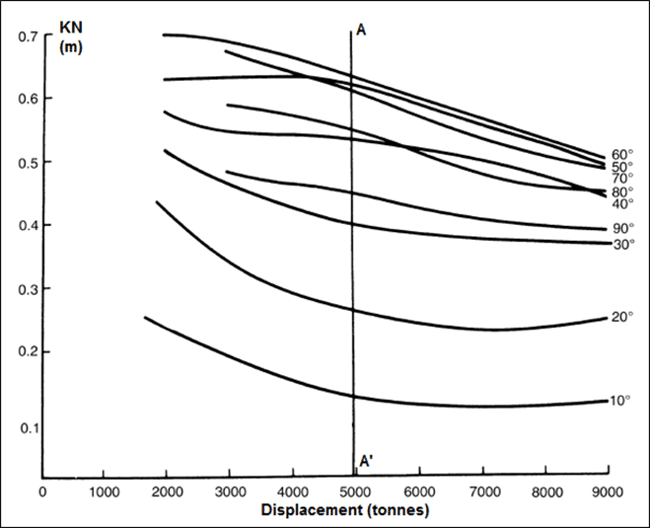
Once the KN curves are obtained, it is now possible for the designer to obtain the stability curve / GZ curve for any loading condition. How?
First, the loading condition is set, and the corresponding vertical center of gravity (KG) is obtained. The displacement of the ship for a particular loading condition is also available (from the hydrostatic curves). Once the displacement is fixed, a vertical line is drawn at the corresponding displacement on the KN curve. For our case let’s assume that the displacement for the given loading condition is 5000 tonnes. So, the line AA’ is drawn through the KN curves, at 5000 tonnes. The value of KN at each angle of heel is then replaced in the expression above, to obtain the GZ at each angle of heel. Once that is done, the designer obtains the GZ versus angle of heel values, which can be plotted to obtain the stability curve for a particular loading condition.
Thus, the KN curve enables us to obtain the stability curve at any predetermined, as well as new loading conditions. It is due to this reason, KN curves are also provided in the Stability Booklet of a ship, so that, in case the ship is operating in a loading condition it hadn’t operated in before, the GZ curve can still be obtained easily to determine the stability of the ship.
You must have found this article to be more theoretical than the previous ones on stability. The reason why we discussed this, it is the ability to play with curves of stability that will allow us to assess practical stability cases with ease. Stability curves can also get tricky a lot of times. We will raise some of those questions here, and answer them in our next article:
- You must have heard the terms – rolling, angle of list, and angle of heel. All three are used for angles made by the ship to the vertical, in the transverse direction. But are they different from each other?
- A ship has an angle of loll. To correct it, should we shift weights within the ship to bring it to an upright position?
- A ship has a list to the starboard side. To correct the list, should we shift weights to from starboard to port side to upright the ship?
- A ship carrying timber wood on its deck has developed a list to port side. To correct the list, the deck cargo should immediately shifted from port to starboard. True or False?
- We’ve only discussed till now, how a positive and higher metacentric height (GM) is preferable for a ship to be stable. But, is a very high GM preferred? Or do designers always try to achieve a fine balance?
Do you have info to share with us ? Suggest a correction
Latest Naval Arch Articles You Would Like:
Subscribe To Our Newsletters
By subscribing, you agree to our Privacy Policy and may receive occasional deal communications; you can unsubscribe anytime.














Hi sir
After painting the touch up on the deck using primer ,second coat and final coat in few months the rust caming again in same places which maintained .
I would like to ask if there is special paint using for protect the deck before using primer ,second and final coat for no return back same rust in same place which maintained.
For your information after touch up the spots by using chipping hamer machine we broshed and used rust remover and washed by fresh water before apply primer.
If there is an other way how to protect the deck.
All the best
Captain Amine
GOOD DAY SIR.THANK YOU FOR YOUR NICE WRITING.WOULD YOU PLEASE EXPLAIN WHY INITIAL GM IS MEASURED IN 57.3 DEGREES.HOPE YOUR NICE AND QUICK RESPONSE.ALL THE BEST.
All the best
@Zaw Zaw Min: Thank you for your wishes
Mr. MOHAMMAD MOKTARUZZAMAN
GM is taken in 57.3 degree because, 57.3 degree equals one radian.
Sir please explain the affect of ships length on GZ curves