Intact Statical Transverse Stability Of Displacement Vessels

In the deep devastating seas where a mere human has no significance, ships’ creation braves through the waters. Ships are one of the biggest accomplishments mankind has ever achieved. Safety is one of the key aspects of these marvellous creations, which is greatly achieved through its stability.

Stability, in simple words, is the ability of a ship to sail in waters without capsizing or being overturned; being neither too tender, nor too stiff despite the various internal and external heeling, listing, trimming, turning and bilging factors. A ship is stable when the net force and the net moments of these forces exactly cancel out according to the laws of vectors analysis. The weight of the vessel is balanced by the fathoms-deep oceans itself. These two forces are aligned exactly opposite to each other, nullifying each other’s moments. The concern of stability arises when the unbalanced external forces are exerted or when the weights within the ship are moved in an unplanned fashion. The moments created are huge and tend to capsize the ship.

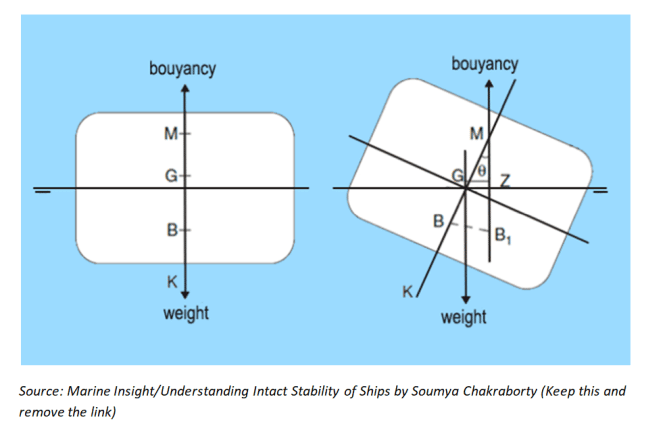
A displacement vessel floats in water in accordance with the Archimedes’ principle which states that, if an object is immersed in a liquid, it experiences an upward thrust, called the buoyant force which is equal to the weight of the fluid displaced by the immersed body. This force acts on the centroid of the immersed body. For a ship, the centroid of its immersed portion is its centre of buoyancy. As the ship heels, lists or trims a capsizing moment is created due to the factors like free surface effect, shifting of weights onboard, effects of winds, effects of icing, loading of cargo or bilging. As a result of the underwater centroid shifts from its original position to counter the effects. This is where good design is required to effectively counter these moments of upsetting forces.

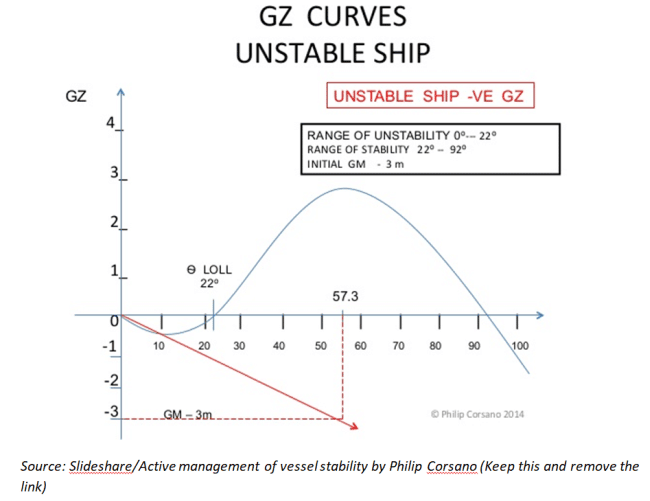
Stability calculations of a ship require the identification of four important points: keel of the ship (K), centre of buoyancy of the ship (B), centroid of the ship (G), and metacenter of the ship (M). The distance GM is termed as the metacentric height. A positive metacentric height is required to produce torque by the virtue of a buoyant force which can counter the upsetting net torque. For an initial negative metacentric height, the ship would initially get stable at the angle of loll.

If a ship returns to its original position after the external force is removed, the ship is well designed and is said to possess a stable equilibrium. Huge righting moments arise due to the upsetting moments and keep the ship from capsizing. The measure of the stability of a ship can be estimated fairly by the length of its righting lever, conventionally denoted by GZ. When a ship is wall-sided, i.e., no part of the deck is immersed in water and no part of the bilge is out of the water, the righting moment arm length for a ship for angles (x) roughly up to 250 is given by the WALL- SIDED formula:

GZ= sin x [GM + 0.5 BM tan2 x]

GZ cross curves are used to determine the righting lever arm length to determine the GZ values at different displacements of the vessel for different angles. The same measure GZ also provides us with the ability of a ship to capsize by its weight by the slightest of heel or list if the location of metacentre is below the centroid of the ship. Plotting the GZ curve requires the knowledge of the location of GM. As the vessels’ loading conditions differ from a voyage to voyage, another curve that is the righting lever arm length measured from the keel of the vessel is plotted. As the keel is uniquely identified for a ship and is a property of ship and independent of the loading conditions, KN cross curves are legit for all voyages. GZ and KN curves are related as:

GZ = KN – KG sin x

Read the full article on the Navisieger magazine here

This article is authored by Rajiv Ratna Jha and was originally published at the inaugural issue of Navisieger. Navisieger is a magazine published by Learn Ship Design. It is a confluence of insights on the maritime technology sector taken from academic experts, naval architects, industry veterans in this field, in the form of articles and exclusive interviews. Learn Ship Design is the first student initiative in India that works towards enhancing industry-academia engagements in the maritime sector.

Do you have info to share with us ? Suggest a correction