Understanding Vessel’s Hull Speed And Its Determination
Whenever we think of the term ‘hull speed’, these are the few things that immediately pop into our minds: It is the maximum rated speed of the vessel; it is the service or the design speed of the vessel; or it is the current speed at which the ship is cruising. These are not the case!
A hull speed is a different hydrodynamic concept and stems from the complex physics of the interplay of the vessel with the surrounding water medium.
Before continuing into this article, it is important to know that hull speed is quite a complicated topic that requires a deep understanding of hydrodynamics and ocean-level wave mechanics but can be somewhat simplified from its physics point of view for everyone’s understanding.
Moreover, we shall first discuss everything from the assumption of the displacement type hulls, which are the simplest and commonest vessels and relies on the basic Archimedes’ principle of displacement and buoyancy.
To begin with, as the vessel moves in water, it is encumbered by the continuous reaction of the water around it. In a technical sense, this is the hydrodynamic resistance suffered by the moving body and is often further divided as
i) frictional resistance originating from the viscous effects of the water with the hull and
ii) the wave resistance due to the various waves associated with the vessel’s movement and the existence of the waves in the water itself.
Thus, to sum it up, a moving vessel is inevitably associated with a system of wave patterns. These waves can be of various types and is a huge topic of hydrodynamics altogether, but for all practical purposes, a moving vessel broadly creates two wave patterns, also known as wave trains.
These are transverse and longitudinal. Transverse waves essentially move in a direction transverse to the vessel’s moving direction, and longitudinal ones traverse in a direction from bow to sternwards or from front to aft.
Now, these longitudinal wave systems are mostly triggered by the kinetic energy of the moving vessel, and thus, this increases quadratically with the vessel’s speed of advance. The transverse waves are less triggered by this kinetic energy as they have their component of motion completely perpendicular to the vessel’s advance.
Now, as this kinetic energy gets transferred to the water medium (ice effects are ignored and beyond the scope of this article), there are two things happenings:
- The vessel is losing its energy of motion.
- The waves are gaining energy from this transferred kinetic energy, and this is further hindering the forward motion of the vessel.
Thus, the vessel’s dynamics have to work up against these waves constantly. For a simple example, consider a simple and unpropelled floating body like a fisherman’s boat in choppy seawater. Imagine that it is being imparted to a large one-time force in the forward direction.
You will notice that the boat surges for some time in the direction of the applied force and then comes to a halt. This is because the kinetic energy gained momentarily is gradually attenuated due to the action of the waves, and the boat stops after attaining dynamic equilibrium.
Now, for a vessel with a constant power source like a ship, the forces continuously supplied by the engine work to overcome this loss of kinetic energy due to the waves, and the vessel continues to surge forward. Here the engines essentially compensate for the energy loss from the waves to maintain the vessel at the given speed. But this comes at the expense of an excess amount of power required and fuel consumed. Why?
The answer lies in the hydrodynamics associated with the waves themselves.
Reiterating what we have discussed above, the motion of a vessel in water leads to the formation of a system of linear and transverse waves that cause wave resistance and absorbs the kinetic energy of the moving vessel.
In technical language, this collective effect of waves is known as standing waves. These waves are time-varying oscillations where the peak amplitude, also known as the crests, changes with time but are not varying in space.
We omit further discussing these waves with the knowledge that they are constantly interacting with the vessel as it tends to surge ahead. From the point of view of the moving vessel, these patterns of waves are also collectively known as the wake.
The wake is responsible for this loss of dynamic energy of the vessel, and the latter needs to stave off these wake effects to move forward. However, due to the constant building energy from the transferred kinetic energy on these waves, the vessel faces further hindrance or resistance that needs to be overcome at the expense of a higher value of energy if it is to continue moving ahead.
From the nature of the mechanics of these waves, they move at a velocity of square root [(acceleration due to gravity X wavelength)/(2Xpi)].
It can be symbolically expressed as (gλ/2π)^(1/2)
Where g is the acceleration due to gravity (9.8m/s2), λ is the wavelength of the surface wave, and π is the mathematical constant pi which is 3.14.
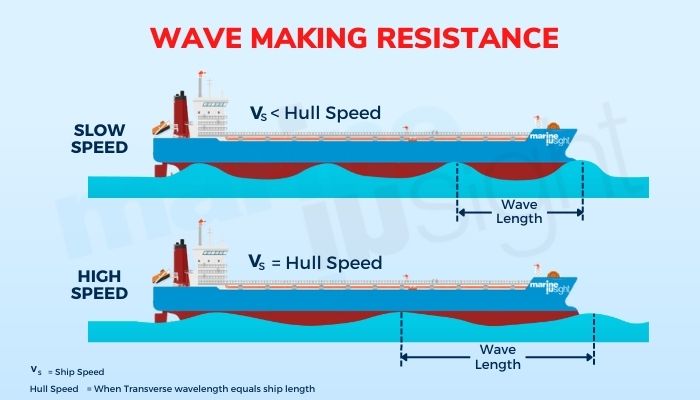
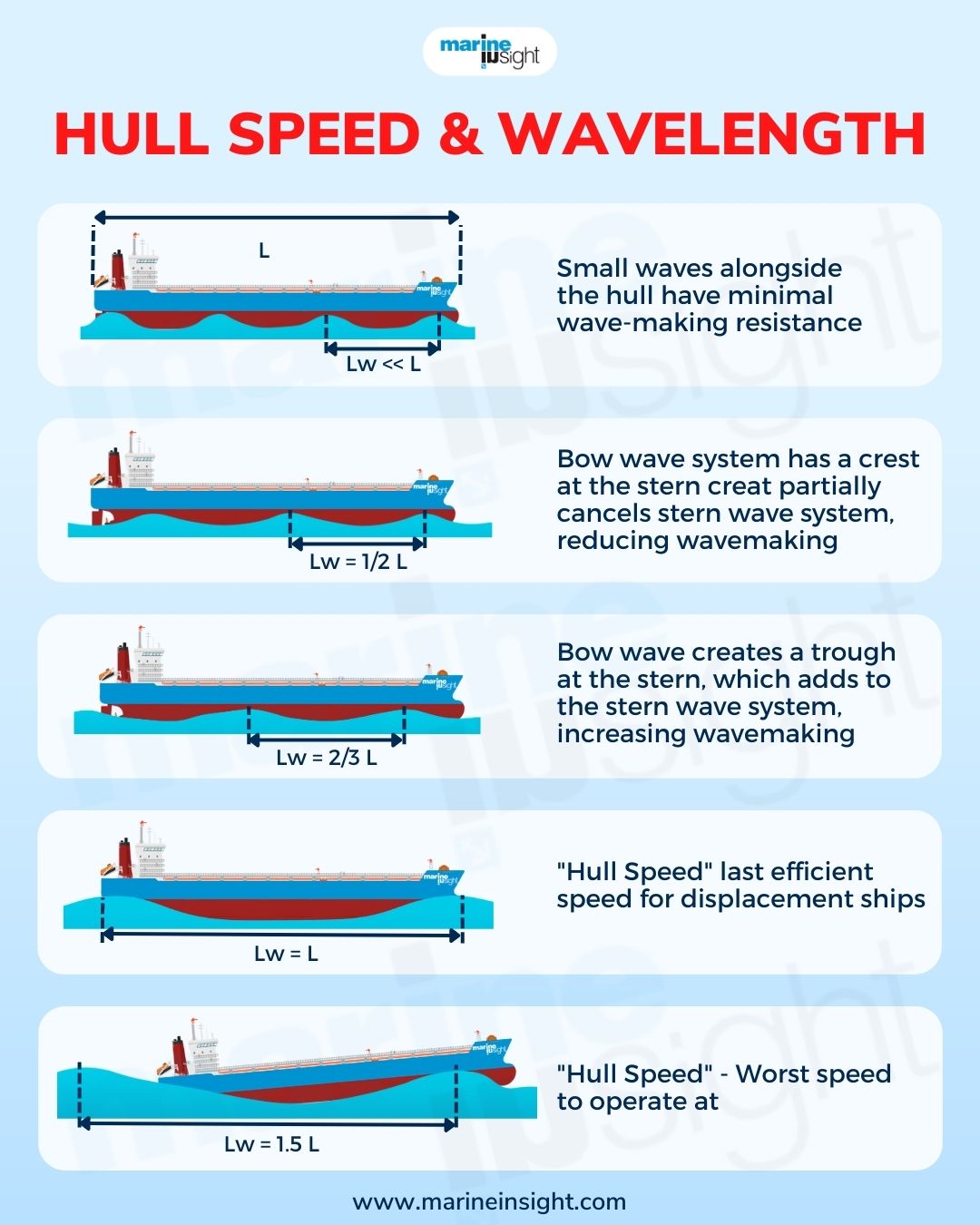
Suppose a vessel has a length of L, and the created wavelength is λ. The number of crests and troughs along the hull of the vessel is L/λ. This is the length of the vessel divided by the wavelength. As seen from the profile, the first crest is always generated near the bow, known as the bow wave.
Now, two scenarios occur.
- The vessel does not impart any further force, like the previously discussed fisherman’s boat example. In this case, the vessel experiences a loss in energy and comes to a gradual halt when the dynamic equilibrium is attained, that is, the dynamic energy of the passing wave train is equal to the initial kinetic energy of the vessel.
- The vessel continues to supply energy like in powered ships. And after a certain point of time, its velocity becomes equal to the wave velocity.
In both cases, when there is this energy equilibrium or a kinetic equilibrium, the speed at which this occurs is known as the hull speed or critical speed. Now, at this value of speed, the wavelength becomes essentially equal to the length of the vessel. And the vessel’s speed becomes equal to the wave speed.
Conversely, the hull speed is the maximum speed or the limiting speed at which an unpowered vessel will not experience a loss in speed or at which a powered vessel will continue surging without an added expense of power. In the latter case, after exceeding this critical value of speed, the increase in wave resistance is now at an exponential rate. This translated to a very high expense of power to attain further increments in speed.
Look at the below graph. After the hull speed value, for a conventional monohull-powered sea-going ship, the energy expended to attain higher speeds now escalates exponentially instead of quadratic.
This can be simply explained by the physics of relative speed. As the vessel’s surge exceeds the speed of the waves, the relative velocity between the two becomes negative. The wave now cannot outrun the vessel’s speed tendency. As a result, there is a great deal of energy build-up at the bow region and many crests at the aft instead of crests.
In more languages of physics, the wave trains now become out-of-phase with the ones initially generated. Hydrodynamically, this leads to a dramatic increase in induced values of wave resistance. Moreover, due to the wave train build-up at the bow area, the vessel tends to lose buoyancy support at the stern. In technical terms, this is also known as squatting effects or squat.
So, in the simplest of terms, hull speed can alternatively be described as the maximum speed at which the vessel continues to accelerate or surge without facing significant losses or expenses in power.
Recall the expression of velocity mentioned above. As in the case of hull speed, the wave speed becomes equal to the vessel’s speed. The hull speed can be further mathematically expressed as: 1.34 times the square root of the vessel’s length, simplifying the above terms and replacing the wave speed term with the given vessel’s speed as both are equal.
So, hull speed can be numerically defined as: 1.34 X (L)^(0.5), where L is the overall length of the vessel.
For all practical purposes, commercial vessels, for a very long time, avoid this hull speed and keep their velocities within this limit unless necessary to save on high power consumption.
Now, some vessels, like defence crafts, often ply at speeds much greater than hull speeds due to their special design and high delivery of power from their powerful engines. Smaller boats like speedboats or some motor yachts often tend to avoid this hull speed obstruction by just ‘climbing up the waves’ built up in front and avoiding the bow waves themselves!
Planing and semi-displacement crafts, which uses the physics of lift action, are highly efficient in avoiding the hull speeds and their related effects.
These days, Froude Number, a dimensionless ratio of speed and length, is mostly used for estimating resistance effects and hull-water interaction.
You might also like to read-
- What are Draft Lines Of Vessels?
- What Are Embarkation Ladders?
- What is the Stern Of A Ship?
- What Are Ship Bottom Plugs Or Dock Plugs?
Disclaimer: The authors’ views expressed in this article do not necessarily reflect the views of Marine Insight. Data and charts, if used, in the article have been sourced from available information and have not been authenticated by any statutory authority. The author and Marine Insight do not claim it to be accurate nor accept any responsibility for the same. The views constitute only the opinions and do not constitute any guidelines or recommendations on any course of action to be followed by the reader.
Do you have info to share with us ? Suggest a correction
Latest Marine Navigation Articles You Would Like:
Subscribe To Our Newsletters
By subscribing, you agree to our Privacy Policy and may receive occasional deal communications; you can unsubscribe anytime.
Web Stories

About Author
Subhodeep is a Naval Architecture and Ocean Engineering graduate. Interested in the intricacies of marine structures and goal-based design aspects, he is dedicated to sharing and propagation of common technical knowledge within this sector, which, at this very moment, requires a turnabout to flourish back to its old glory.