Ship Stability: Intact Stability Criteria and Inclining Experiment
Remember, in the first article of this series, we had mentioned that the value of GM needs to be obtained at various stages from design to construction of a ship. We had also mentioned that the purpose to obtain the value of this parameter at different stages differs from stage to stage.
The first time when the metacentric height of a ship is estimated, is during its initial design stages using the following methods:
- Empirical Formulae: A number of empirical formulae have been developed based on results of experiments made on different types of ship hull forms that help naval architects to approach to an expected value of metacentric height based on very basic dimensional parameters, like Length, breadth and Depth of the ship. Though the results obtained from these empirical formulae are not always accurate, they are used to arrive at an approximate value, which is very necessary, since ship design is a closed loop iterative process.
- Initial Hydrostatic Calculations: Once the hull has been designed based on the results obtained from the empirical formulae, it is necessary to calculate the metacentric height using the values of other hydrostatics. The formula used in this stage is as shown below:
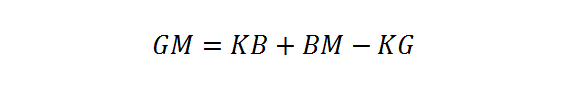
The purpose to calculate the GM at this stage of design is to compare it with the value obtained from empirical formulae, and decide on the requirement of iterations in the hull design. For conventional designs, the percentage difference between the two would be within 2 to 3 percent. However, in case of novel designs, the values obtained at this stage is solely reliable, not the ones obtained from empirical calculations.
This article will discuss about the other two stages of ship design and construction where evaluation of GM is an absolute necessity and plays a major role in ensuring that the ship is stable, and built as per the requirements of the client.
Stability Criteria:
A number of criteria that are based on the shape and nature of the stability curve of a ship, are used to evaluate the stability of a ship. Remember, that since we are discussing about intact stability, we will only focus on intact stability criteria, i.e. to evaluate the point where the ship becomes unstable, the values of certain parameters will be obtained from the stability curve pertaining to the least favorable loading condition.
Some of the features of the stability curve that are studied here are:
- The steady heel angle in case of any heeling moment (wind moments, grain shift moments, etc.) This angle is shown in the following figure, at the point of intersection of the heeling curve and static stability curve. This angle plays a major role not only in determining the safety of crew, personnel, and cargo on board, but also helps in determining the angle at which the deck edge of the ship is likely to submerge. In other words, it helps us evaluate a ship’s resistance to capsizing, for a given loading condition.
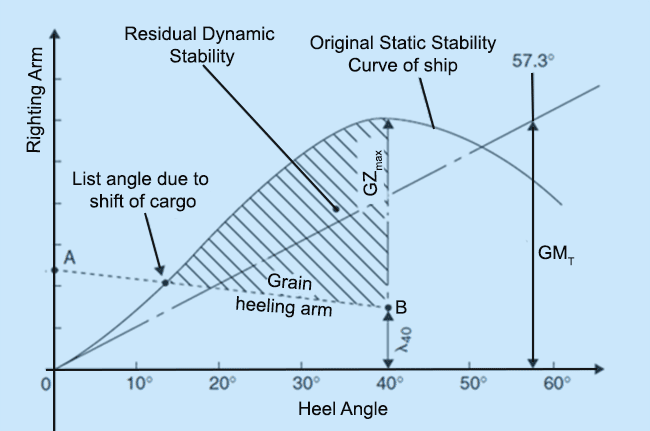
- The range of positive stability for each loading condition. It is important to know this parameter because it gives us the angle upto which the ship can heel before capsizing.
- The magnitude of the heeling arm relative to the righting arm for every loading condition. The available difference between the righting and heeling arm gives us the allowable margin for further upsetting forces (wind, waves, etc.) before the ship attains negative stability.
Some of the criteria used to assess stability of a ship are also based on the dynamic stability of the ship. So, what is dynamic stability? Whatever we have discussed in the previous articles on stability, we have only dealt with Static Stability, i.e. stability of a ship when it is static. You could imagine it as if you have photographed a ship that is heeling, and studied its stability for that static condition in the photograph. However, dynamic stability deals with the study of stability over a range of angle of heels on the curve of intact stability.
For any given angle of heel, dynamic stability is the measure of the work done in heeling the ship to that angle, very slowly and while maintaining constant displacement. This is measured by the area under the static stability curve upto that angle, as shown in the figure below, where the grey shaded area is the dynamic stability of the ship at 30 degrees of heel.
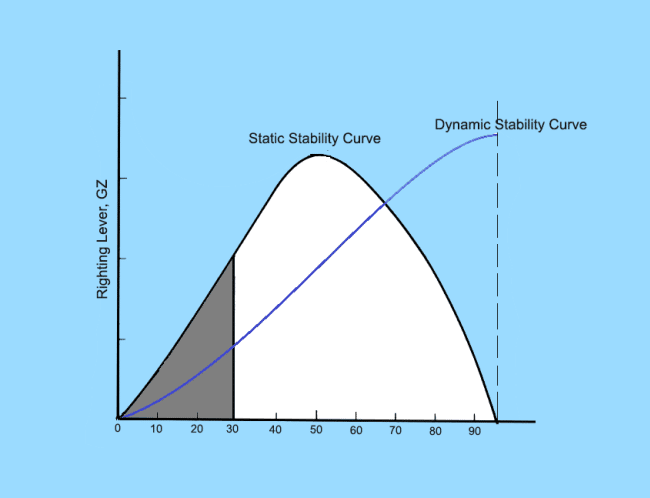
So if at every angle of heel, the area under the static stability curve upto that angle is plotted, the curve for dynamic stability is obtained, which is shown in blue. This curve plots the amount of energy that the ship can absorb in order for it to heel upto a certain angle.
As per as dynamic stability criterion is concerned, we are more interested in evaluating the Residual Dynamic Stability of the ship in the following conditions:
- Shift of cargo within the ship.
- Presence of wind heeling moments.
- Wave heeling actions.
- Lifting of weight over one side.
All the four above cases result in a heeling moment which can be plotted similar to that in Figure 1. The area between the heeling moment curve and the righting moment curve (curve of static stability) is the Residual Dynamic Stability, and is less than the Dynamic Stability in absence of any of these upsetting forces. This value is evaluated for every loading condition and is tallied with a criteria set by governing bodies.
There are various international and national governing bodies that have established a set of criteria for ensuring adequacy in stability of ships. Some of these bodies are:
- International Maritime Organization (IMO)
- US Coast Guard (USCG)
- American Bureau of Shipping (ABS)
- Directorate of Naval Design (DND), Indian Navy
DND, India has set a series of stability criteria that are to be complied with, by all the ships serving for Indian Navy and Indian Coast Guard. Information regarding the same is classified, and hence, out of the scope of this article.
Our focus will be on the criteria set for merchant ships that ply on national and international waters. These criteria are laid down by International Maritime Organization (IMO) in The IMO Code of Intact Stability for Merchant Ships. This code specifies the formulae that are used to calculate:
- Heeling arm due to winds and rolling.
- Heeling arm due to grain shift or shift of dry cargo.
- Heeling arm due to crowding of passengers on one side.
- Heeling due to high speed turn.
The above four parameters are used to plot the heeling arm curves for each condition. The GM values are calculated by carrying out stability calculations at each loading condition considering reduction in metacentric height due to free surface effect. The results are all plotted on a stability curve. The values obtained from the curve should follow the following stability criteria for all merchant ships:
- The area under the GZ curve must not be less than:
- 055 meter radian up to 30 degrees.
- 09 meter radian up to 40 degrees or the smallest angle of heel at which flooding takes place through openings (this angle is called the Downflooding Angle).
- 03 meter radian between 30 to 40 degrees or the downflooding angle (whichever is the least).
- Righting arm (GZ) must be greater than 0.20 meter at 30 degrees.
- Maximum righting arm should occur at an angle more than 30 degrees.
- Minimum metacentric height should be 0.15 meter.
The criteria mentioned above, are however, only a part of all the criteria mentioned in the code. If any criteria is not complied with, required changes are to be made in the loading conditions or tank capacities, or tank positions, depending on the criteria and which stage of design it is.
The Inclining Experiment:
An inclining experiment is carried out when the construction of the ship is completed up to a stage when all the components that contribute to the lightship weight have been installed. The primary purposes for carrying out an inclining experiment are:
- To measure the lightship weight of the ship.
- To find the vertical, longitudinal, and transverse positions of center of gravity.
- To calculate the metacentric height of the lightship.
It is always conducted by the shipbuilder because, at this stage, the shipbuilder must prove to the client that the lightship weight has not exceeded the design value. This is a very important milestone for the shipbuilder because, often, marginal increase in weight is likely to be observed due to various manufacturing constraints. It is due to this reason, a weight margin of approximately 15 to 20 percent is allowed in the technical contact. However, if the difference between the design lightship weight and that calculated during the inclining experiment exceeds weight margin mentioned in the contract, the shipbuilder must pay a penalty for each extra ton.
The experiment is carried out by inclining the ship using known weights. The known weight is first shifted to one side of the ship, and the inclination is measured by means of under deck pendulums placed at various longitudinal positions along the center line of the ship. The bobs of the pendulums oscillate on battens with readings marked on them. The length of the pendulums are usually about 10 to 12 meters, and they are submerged in oil or a dense fluid so as to increase damping.
When the ship is ready for the experiment, the weight is shifted on the deck in a transverse direction. This causes the ship to list. The ship is first allowed to settle down in this position and the deflection on the battens are measured on all the pendulums. The mean deflection is then calculated and considered as the value to be used for calculations. The same process is repeated by shifting the weight to the opposite side. In some cases, multiple observations are taken using different weights.
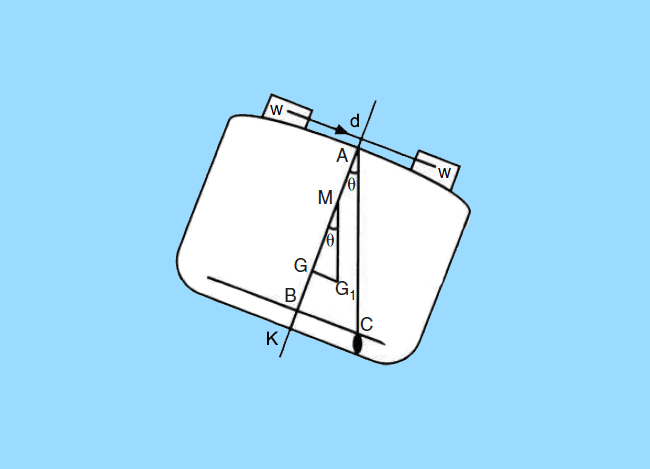
The above figure shows an inclining experiment in which a known weight of ‘w’ tonnes has been shifted by a distance ‘d’. The deflection of the pendulum is read as ‘BC’ on the horizontal batten. As a result of shift of weight on the ship, the center of gravity of the lightship shifts from ‘G’ to ‘G1’.
The metacentric height can then be calculated using the following expressions:
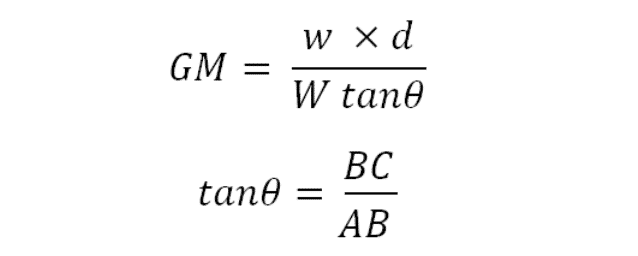
Where, ‘W’ is the measured mass displacement of the ship; AB is the length of the pendulum used; BC is the mean deflection read on the batten.
There are a number of precautions required to be taken in order to attain fairly accurate results, and they are to be ensured by the shipbuilder before the experiment commences:
- The experiment should be carried out when no beam winds are present. In case beam winds are unavoidable, corrections of metacentric height for beam winds are to be incorporated into the calculations.
- The ship must be floating upright at zero heel angle, and must not be restrained by mooring ropes.
- All lose weight present inside the ship should be restrained. Often, a lot of temporary structures like scaffoldings, wooden platforms, welding machines, etc. are present inside the ship during the experiment. They are either to be removed, or to be fixed to the ship so that they do not shift during the experiment. In the second case, their weights are to be recorded and the weight of the ship ‘W’ is to be corrected accordingly for calculations.
- Tanks should either be emptied or pressed to full capacity. In case none of that is possible, the level of liquid in the tank should be such that free surface effect is minimum, and corresponding free surface corrections should be made in calculation of the metacentric height.
- There are a number of personnel who are required to be on-board during the experiment. The number of personnel is to be kept to a minimum, and they are supposed to take pre-decided positions on the ship (which is usually along the centerline) before the readings are taken.
- All interconnections between tanks should be closed, irrespective of whether the tanks are empty, fully pressed, or partially filled.
- The draft marks of the ship must be read before the experiment begins, so as to ensure design trim and absence of a condition of loll.
- The density, salinity and temperature of the water on which the ship is floating, must be measured and recorded before the experiment. This density must be used to calculate the mass displacement of the ship ‘W’. It is always recommended that the experiment is carried out in sea water.
Though the stability characteristics of a ship can be determined with considerable precision, most authorities and shipbuilders find themselves in a trap while quoting the primary characteristics like metacentric height and righting lever with great accuracy. This is because, a design cannot be replicated to the fullest, in the real world. Hence, a naval architect must be aware of the following reasons that often cause the real-time values to vary from the design values:
- Ships are not built exactly according to the lines plan, because the curvature of plates is almost always not achievable as per the lines plan. There is always a difference of 0.1 to 0.3 percent in the curvature, which when scaled up to the size of the ship, creates a shift from design values.
- The weights and center of gravity vary within a margin, due to the contribution of plate thicknesses and added weight due to welded joints.
- The accuracy of the actual KG of the ship as assessed, depends largely on the level of accuracy involved in the inclining experiment. It is based on the results of this experiment that the stability booklet of the ship is updated, and further stability parameters are calculated.
- One of the most important assumptions in all the stability calculations are that the ship is floating in an even keel or zero trim condition. However when values are recorded in real life, they are done in design trim conditions, and not at even keel. This results in a visible difference between design and practical values. However, recent design software are capable of carrying out all stability analyses in required trim conditions, which shoots up the level of accuracy.
All that we have discussed till now is, the stability of a surface ship when it is intact. How is the stability of a ship affected when its hull is damaged? How is a ship designed to be safe even if one or two compartments are completely flooded? These are aspects that fall in the category of Damaged Stability of Surface Ships, which we will be our topic in the next article of this series.
Do you have info to share with us ? Suggest a correction
Latest Naval Arch Articles You Would Like:
Subscribe To Our Newsletters
By subscribing, you agree to our Privacy Policy and may receive occasional deal communications; you can unsubscribe anytime.













excellent
How to calculate known weight ?
When G1G2 & LBP is not given, and we’re asked to find the GM of a vessel, do we use:
GM = (w × d × Original Length) ÷ (Displacement × Deflection); to find the answer?
Like say for example, a vessel with the displacement of 4950 t, which is initially upright when a weight of 25 t is moved across the deck 9.14m and at the same time a plumb line of 4.26m in length is deflected 0.3m. Find the GM.
GM = (w × d × Original Length) ÷ (Displacement × Deflection)
= (25t × 9.14m × 4.26m) ÷ (4950t × 0.3m)
= (973.41) ÷ (1485)
Therefore, GM = 0.655 m.
We didn’t really cover this topic well in class so I don’t know if I did the correct thing to find the answer (GM).
tan theta is BC/AB NOT AB/BC…
corrected Deepak. Thank you for keeping a sharp eye.