What is Angle Of Loll in Ships?

Transverse statical stability is the ability of the vessel to remain upright under the influence of various external and internal factors. Transverse stability, as we know, is only considering the stability aspects in the transverse sense or the longitudinal direction.

Going back to the basics, when a vessel suffers an internal or external disturbance from a lateral direction, it tends to heel or list towards a particular side. Once again, the heel is the inclination caused by external forces, and the list is due to the transfer of internal weights.

The inclination is measured in terms of the heel angle. The most important points to consider while analysing initial intact stability are the centre of gravity, G, the centre of buoyancy, B, and the metacentre, M. While understanding the metacentre. It is important to go back to the initial conditions of stability. <Refer article>.

So, the metacentre is the point of intersection of the ship’s centreline, with the line passing through the centre of buoyancy when the vessel has been inclined. Alluding and reiterating back to the initial conditions of stability, if the transverse metacentre is vertically above the centre of gravity, the ship is said to be in a stable or equilibrium state if the transverse metacentre is vertically above the centre of gravity.

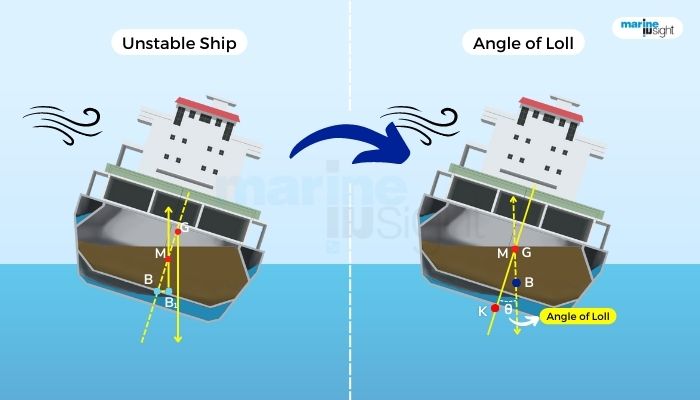
Angle Of Loll

If the metacentre coincides with the CG, the vessel is said to be in a neutral state. And if the metacentre lies below the CG, the vessel is said to be in an unstable state. When the vessel is inclined, a righting lever or arm tends to bring the vessel back to its upright position by its righting moment. The length of this arm is a direct determinant of the righting moment.

Now, initial stability may be under two types of study: 1) stability at large angles of inclination and 2) stability at small angles of inclination. While considering small inclination angles, it is usually taken as within 4 or 5 degrees. However, when the angle of the heel or list is greater than 4 or 5 degrees of radius, it is taken under the purview of large angles.

This is because, technically, when the angles of inclination are greater than this, the metacentre M does not remain a fixed point but dynamical. Furthermore, it can no longer be considered a measure of stability and somewhat altered and more complicated formulations and calculations for stability come into play.

So, the determination of the righting lever for these instances requires special consideration and can be estimated using relations like Atwood’s formula or the Wall-sided formula, which is a special case of Atwood’s. We do not get into the formulations and other aspects as they are beyond the scope of this article.

Now, for stability at large angles, a very interesting case arises. As we already know from the first principles of stability, the righting arm or lever can either be positive, negative or zero. A positive righting arm creates a positive righting moment that tends to bring the vessel to an upright position from an unstable position. In contrast, a negative righting moment further pushes the vessel to heel or list towards its side.

Angle Of Loll

For the zero righting lever, the case is quite complicated. When the metacentric height or GM is positive or zero, the lever arm can still be zero, and the vessel is said to be in equilibrium. Here, the ship shall essentially remain in its position without heeling further but, at the same time, not tending to get back upright since there is no moment arm to give rise to the crucial moment required.

Still, the vessel can be considered more or less ‘stable’, thanks to the positive GM or, in other words, the location of the metacentre being above the centre of gravity, as we know. However, when the vessel has a zero righting arm and a negative GM, there can be a very special case that cannot be considered an unstable state. Here, the vessel shall attain a state where it will be in equilibrium but never attain so! Sounds strange, right? But it happens in this case.

Since the GM is negative and the BM is positive, the vessel will never capsize but shall tend to remain in a state of oscillation, that is, to and fro. There shall not be a preference for the vessel towards any particular side. The angle of inclination of the vessel under given conditions at which this occurs is known as the angle of loll, and the vessel is said to be in a state of continuous rolling motion.

Due to the absence of a stabilising righting lever coupled with a negative GM, the vessel shall never attain the desired stability or uprightness. This is also known as the state of unstable equilibrium.

Unstable in the sense that it never attains the desired position, and equilibrium in the sense that even though it does not, it remains in a state that does not incline partially to one side continuously and capsizes. However, during this incessant state of oscillation, if there is water ingress on the deck due to some reason, the vessel may capsize due to added loads and forces.

The angle of loll for a given vessel under given conditions can be determined mathematically by the values of GM, the metacentric height and BM, and the metacentric radius.

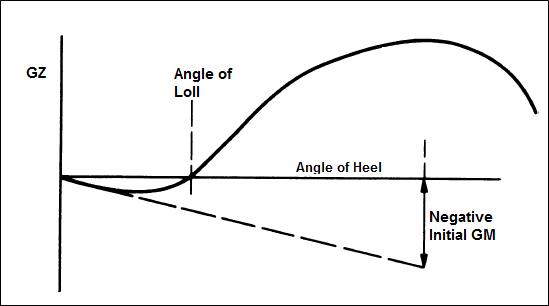
As per the GZ curve, the angle of loll occurs at the inflexion point when the GZ or the righting lever becomes zero while transforming from a negative value to a positive value. The other points on the curve where the GZ is zero are when the ship is in a natural upright state that is not disturbed by any force and has zero angles of heel, and the end of the stability curve which is also known as the angle of vanishing stability.

The metacentric height or the GM is twice in magnitude and opposite in sign or direction under a lolled condition. We do not get into the detailed calculations here in this article.

This state of continuous oscillation or rolling is quite precarious for passengers and crew. It may induce severe problems like seasickness, damage to equipment/systems or loss of cargo and other items.

The condition worsens further during inclement weather conditions when the sea state is already disturbed, and the vessel is already subject to many disturbances. Under such conditions, there are real chances of the vessel capsizing. The angle of loll is a very important consideration to a designer right from the beginning.

Several systems, like anti-roll tanks or other anti-roll devices and mechanisms, are common in most modern vessels to counter rolling motions. However, ships always take care to avoid this angle of loll for all practical purposes.

You might also like to read-

Do you have info to share with us ? Suggest a correction

About Author

Subhodeep is a Naval Architecture and Ocean Engineering graduate. Interested in the intricacies of marine structures and goal-based design aspects, he is dedicated to sharing and propagation of common technical knowledge within this sector, which, at this very moment, requires a turnabout to flourish back to its old glory.