Inclining Experiment- Determining Metacentric height of the ship
The Metacentric height of the ship plays an important role in setting the loading capacity and stability of the ship. The Initial metacentric height of the ship is determined by an inclining experiment after the ship is completely built.
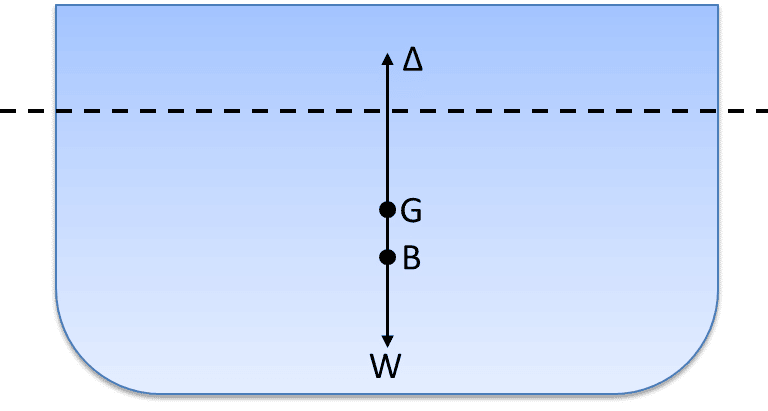
Metacentre and Metacentric height
As discussed in our previous article Understanding Intact & Damage Stability of Ships, lets consider a ship which was in eqilibrium is now inclined by an angle Ѳ.
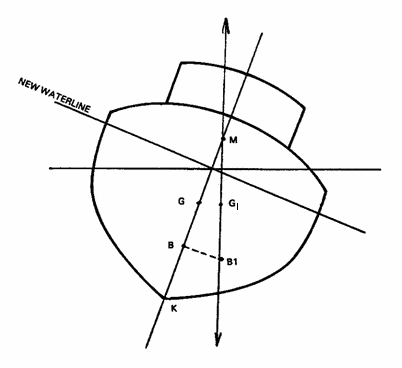
When a ship is heeled by an angle, the center of buoyancy is shifted from B to B1.
When a vertical line is drawn from B and B1, they intersect at a point known as metacentre of the ship.
The metacentric height is the distance between the centre of gravity and metacentre of the ship i.e. GM and it is used to calculate the stability of the ship.
Inclining Experiment
Requirements
- The experiment is carried out when the ship is built completely or when major structural changes have been done.
- The experiment is carried out with empty ship or as near to empty ship as possible.
- The ship must be in upright position.
- The ship should be sheltered and in calm waters.
- Mooring ropes should be slackened and gangway lifted.
- Draught and density of water are to be correctly noted.
- All tanks in the ship must be empty or pressed up tight to reduce free surface effect.
- Only those people responsible for conducting the experiment must go onboard.
The Experiment
To conduct this experiment, a special tool known as stabilograph is required. The tool consists of a heavy metal pendulum balanced on a knife edge and connected to a pointer to record the heel angle readings.
Normally minimum of two stabilographs are used and are placed at maximum distance from each other i.e. one in forward and one at aft.
Four masses are placed on the ships deck, two on each side of the mid ship, placed away from the centre line.
In the next step, the masses are moved one at a time until all four are on the same side, then all four on the other side, and lastly two on each side.
The deflection on both the stabilographs is recorded for all the movement of mass and an average of these readings are used to determine metacentric height.
Suppose Ѳ is the angle of heel and G1 is the moved position of the centre of gravity after inclination. Then by trigonometry,
GG1= GM tanѲ
Also GG1 is = m x d/Δ
Where m= mass moved
d= distance by which the mass is moved
Δ= displacement of ship in water
Hence GM = m x d /ΔtanѲ
and GM is metacentric height
Where tanѲ can be determined by the readings of stabilograph
You may also like to read-Understanding Intact & Damage Stability of Ships
Reference:
Book on Naval Architecture by E A Stokoe
Do you have info to share with us ? Suggest a correction
Latest Naval Arch Articles You Would Like:
Subscribe To Our Newsletters
By subscribing, you agree to our Privacy Policy and may receive occasional deal communications; you can unsubscribe anytime.
Web Stories

About Author
An ardent sailor and a techie, Anish Wankhede has voyaged on a number of ships as a marine engineer officer. He loves multitasking, networking, and troubleshooting. He is the one behind the unique creativity and aesthetics at Marine Insight.




















This lesson was taught in the Nautical School of Hydra ,in 1956, by our
professor Mr Pallas,visiting us once per week ,learning ”naval architecture” and thanks reminding me the lesson that have never forgotten in my sea life….
thank you very much for the lesson.
can you please tell me where the two stabilographs are exactly positioned while carrying out the inclining experiment.
thnk you
Hey i afraid to inform that i am interested in to the sea life can you please update any clip of how the stabilograph works to my mail id which i have mentioned above thanks…………..it very useful to me
Thanks a lot for the notes. . . In that theory is the application of tan function is correct ???
Or applying sin function would be better ???
Pls respond to me. . . .
Thank you. . .
nice
Reading this publication reminds me of my days in class, it refreshes my memory and gives me better understanding